数据结构 | 串

发表于 2018/04/01 更新于 2024/10/18

作者

次浏览 15 分钟阅读

串的存储表示和实现:

串是一种特殊的线性表,其存储表示和线性表类似但又不完全相同。串的存储方式取决于将要对串所进行的操作. 串在计算机中有3种表示方式:

定长顺序存储方式: 将串定义成字符数组,利用串名可以直接访问串值。用这种表示方式,串的存储空间在编译时确定,其大小不能改变。
堆分配存储方式: 仍然用一组地址连续的存储单元来依次存储串中的字符序列,但串的存储空间是在程序运行时根据串的实际长度动态分配的。
块链存储方式: 是一种链式存储结构表示。

串的定长顺序存储表示:

这种存储结构又称为串的顺序存储结构。是用一组连续的存储单元来存放串中的字符序列。所谓定长顺序存储结构,是直接使用定长的字符数组来定义,数组的上界预先确定。

//定长顺序存储结构定义为:  
#define MAX_STRLEN 256   
typedef struct  
{   
    char str[MAX_STRLEN] ;   
    int length;  
} StringType ;  

//串的联结操作  
Status StrConcat ( StringType s, StringType t)  
/* 将串t联结到串s之后,结果仍然保存在s中 */   
{   
    int i, j ;  
    if ((s.length+t.length)>MAX_STRLEN)   
        Return ERROR ; /* 联结后长度超出范围 */  
    for (i=0 ; i<t.length ; i++)   
        s.str[s.length+i]=t.str[i] ; /* 串t联结到串s之后 */   
    s.length=s.length+t.length; /*修改联结后的串长度 */   
    return OK ;  
}  

//求子串操作  
Status SubString (StringType s, int pos, int len, StringType *sub)   
{   
    int k, j ;  
    if (pos<1||pos>s.length||len<0||len>(s. length-pos+1))  
        return ERROR ; /* 参数非法 */   
    sub->length=len-pos+1 ; /* 求得子串长度 */  
    for (j=0, k=pos ; k<=leng ; k++, j++)  
        sub->str[j]=s.str[i] ; /* 逐个字符复制求得子串 */  
    return OK ;  
}  

串的堆分配存储表示:

实现方法:系统提供一个空间足够大且地址连续的存储空间(称为“堆”)供串使用。可使用C语言的动态存储分配函数malloc()和free()来管理。

特点是:仍然以一组地址连续的存储空间来存储字符串值,但其所需的存储空间是在程序执行过程中动态分配,故是动态的,变长的。

//串的堆式存储结构的类型定义  
typedef struct  
{   
    char *ch; /* 若非空,按长度分配,否则为NULL */  
    int length; /* 串的长度 */   
} HString ;  

//串的联结操作  
Status Hstring *StrConcat(HString *T, HString *s1, HString *s2)  
/* 用T返回由s1和s2联结而成的串 */  
{  
    int k, j , t_len ;  
    if (T.ch)   
        free(T); /* 释放旧空间 */   
    t_len=s1->length+s2->length ;  
    if ((p=(char *)malloc(sizeof((char)*t_len))==NUL L)  
    {   
        printf(“系统空间不够,申请空间失败 ! \n”) ;  
        return ERROR ;   
    }  
    for (k=s1->length, j=0 ; j<s2->length; k++, j++)  
        T->ch[j]=s1->ch[j] ; <span style="font-size:14px;">/* 将串s2复制到</span>串T中 */  
    free(s1->ch) ;   
    free(s2->ch) ;   
    return OK ;  
}  

串的链式存储表示:

串的链式存储结构和线性表的串的链式存储结构类似,采用单链表来存储串,结点的构成是:

data域:存放字符,data域可存放的字符个数称为结点的大小; next域:存放指向下一结点的指针。

若每个结点仅存放一个字符,则结点的指针域就非常多,造成系统空间浪费,为节省存储空间,考虑串结构的特殊性,使每个结点存放若干个字符,这种结构称为块链结构。

串的块链式存储的类型定义包括:

//(1) 块结点的类型定义  
#define BLOCK_SIZE 4  
typedef struct Blstrtype  
{   
    char data[BLOCK_SIZE] ;   
    struct Blstrtype *next;  
}BNODE ;  

//(2) 块链串的类型定义   
typedef struct  
{   
    BNODE head; /* 头指针 */   
    int Strlen ; /* 当前长度 */  
}Blstring ;  

在这种存储结构下,结点的分配总是完整的结点为单位,因此,为使一个串能存放在整数个结点中,在串的末尾填上不属于串值的特殊字符,以表示串的终结。当一个块(结点)内存放多个字符时,往往会使操作过程变得较为复杂,如在串中插入或删除字符操作时通常需要在块间移动字符。

串的查询方法:

package Chap5;

public class BFSearch {
    public static int search(String p, String t) {
        int N = t.length();
        int M = p.length();
        int i = 0; // 主串的索引
        int j = 0; // 字串的索引

        // 若没到任一字符串的末尾，循环之
        while (i < N && j < M) {
            // 字符相同时，索引都加1
            if (p.charAt(j) == t.charAt(i)) {
                i++;
                j++;
            } else {
                i = i - j + 1; // 这句是关键
                j = 0;
            }
        }
        // 跳出循环的时候不是i == N（没找到）就是j == M（找到）
        if (j == M) {
            return i - j;
        }
        else {
            return -1;
        }
    }

    public static void main(String[] args) {
        int index = BFSearch.search("good", "gootgoodgoopt");
        System.out.println(index); // 4
    }
}

KMP算法查找子字符串:

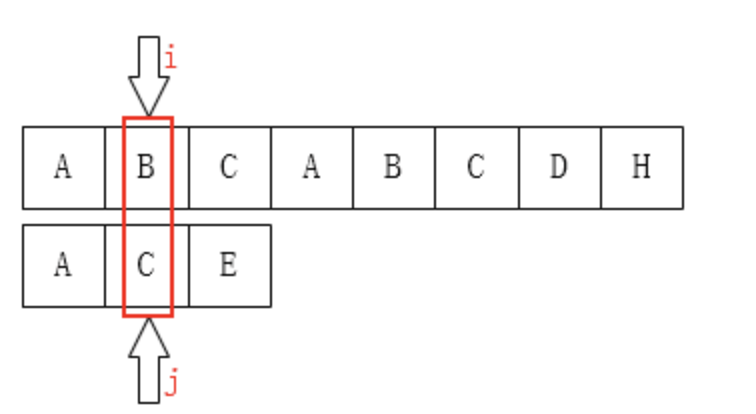
KMP算法的想法是，设法利用这个已知信息，不要把”搜索位置”移回已经比较过的位置，而是继续把它向后移，这样就提高了效率。

整个KMP的重点就在于当某一个字符与主串不匹配时，我们应该知道下次要移动到哪？

接下来我们自己来发现j的移动规律：

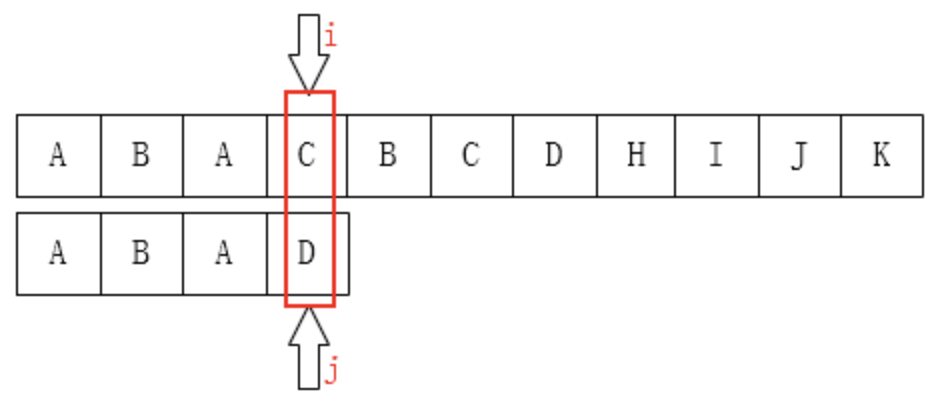
如图：C和D不匹配了，我们要把j移动到哪？显然是第1位。为什么？因为前面有一个A相同啊：

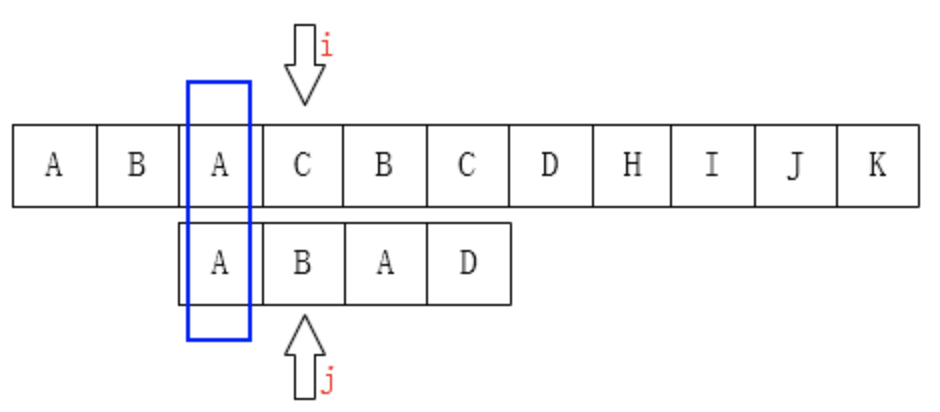
如下图也是一样的情况：

可以把j指针移动到第2位，因为前面有两个字母是一样的：

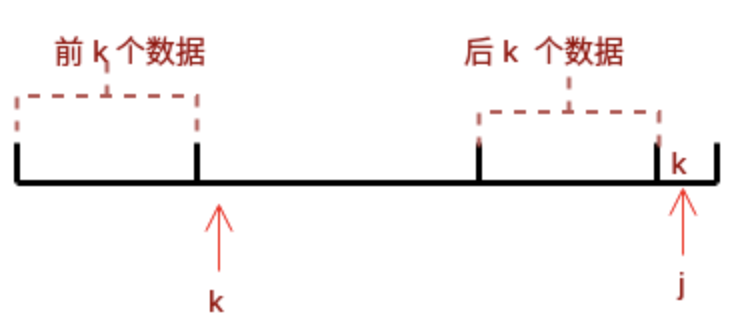
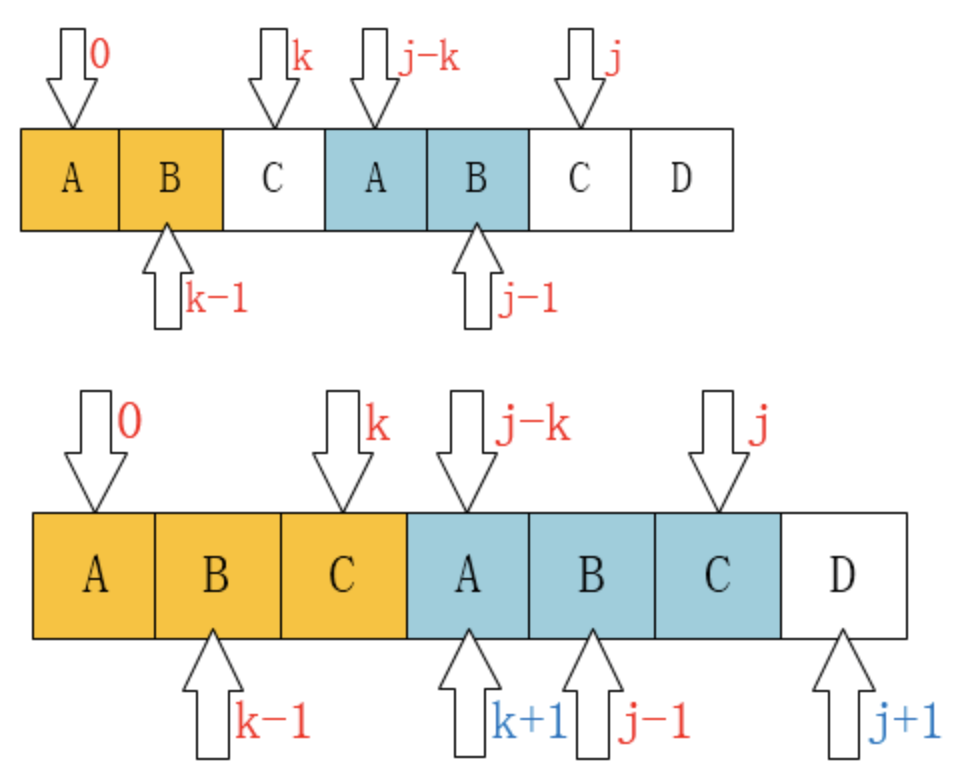
至此我们可以大概看出一点端倪，当匹配失败时，j要移动的下一个位置k。存在着这样的性质：最前面的k个字符和j之前的最后k个字符是一样的。

如果用数学公式来表示是这样的 : P[0 ~ k-1] == P[j-k ~ j-1]

弄明白了这个就应该可能明白为什么可以直接将j移动到k位置了。

好，接下来就是重点了，怎么求这个（这些）k呢？因为在需要匹配的子字符串P的每一个位置都可能发生会与主串T某部分不匹配，也就是T[i] != P[j]. 所以我们要计算每一个位置j对应的k，所以用一个数组next来保存，next[j] = k，表示当T[i] != P[j]时，j指针的下一个位置。

很多教材或博文在这个地方都是讲得比较含糊或是根本就一笔带过，甚至就是贴一段代码上来，为什么是这样求？怎么可以这样求？根本就没有说清楚。而这里恰恰是整个算法最关键的地方。

public static int[] getNext(String ps) {

    char[] p = ps.toCharArray();

    int[] next = new int[p.length];

    next[0] = -1;

    int j = 0;

    int k = -1;

    while (j < p.length - 1) {

       if (k == -1 || p[j] == p[k]) {

           next[++j] = ++k;

       } else {

           k = next[k];

       }

    }

    return next;

}

说明：

当j为0时，如果这时候不匹配，怎么办？

像上图这种情况，j已经在最左边了，不可能再移动了，这时候要应该是i指针后移。所以在代码中才会有next[0] = -1;这个初始化。

如果是当j为1的时候呢？

显然，j指针一定是后移到0位置的。因为它前面也就只有这一个位置了~~~

其他情况:

请仔细对比这两个图。我们发现一个规律：

当$P[k] == P[j]$时，有$next[j+1] == next[j] + 1$

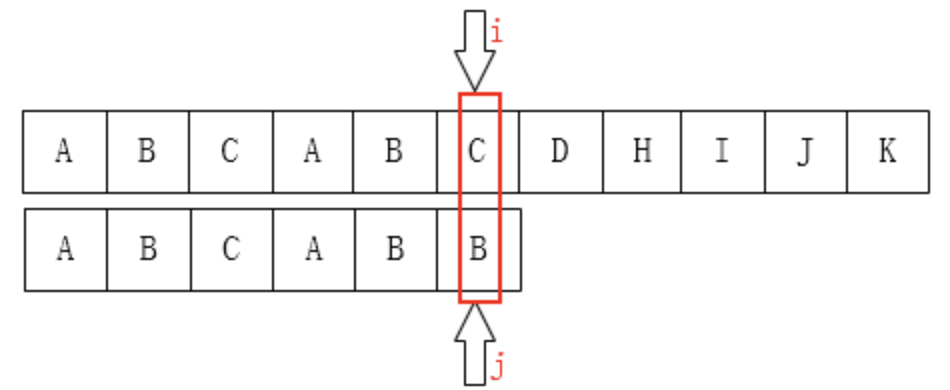
那如果$P[k] != P[j]$呢?比如下图所示：

像这种情况，如果你从代码上看应该是这一句：$k = next[k]$;为什么是这样子？你看下面应该就明白了。

现在你应该知道为什么要 $k = next[k]$ 了吧！像上边的例子，我们已经不可能找到$ [A,B,A,B ]$ 这个最长的后缀串了，但我们还是可能找到$[A,B]$、$[B]$这样的前缀串的。所以这个过程像不像在定位$[A,B,A,C]$这个串，当C和主串不一样了（也就是k位置不一样了），那当然是把指针移动到$next[k]$啦。

有了next数组之后就一切好办了，我们可以动手写KMP算法了：

public static int KMP(String ts, String ps) {

    char[] t = ts.toCharArray();

    char[] p = ps.toCharArray();

    int i = 0; // 主串的位置

    int j = 0; // 模式串的位置

    int[] next = getNext(ps);

    while (i < t.length && j < p.length) {

       if (j == -1 || t[i] == p[j]) { // 当j为-1时，要移动的是i，当然j也要归0

           i++;

           j++;

       } else {

           // i不需要回溯了

           // i = i - j + 1;

           j = next[j]; // j回到指定位置

       }

    }

    if (j == p.length) {

       return i - j;

    } else {

       return -1;

    }

}

和暴力破解相比，就改动了4个地方。其中最主要的一点就是，i不需要回溯了。

优化:

最后，来看一下上边的算法存在的缺陷。来看一个例子：

显然，当我们上边的算法得到的next数组应该是$[-1,0,0,1]$

所以下一步我们应该是把j移动到第1个元素咯：

不难发现，这一步是完全没有意义的。因为后面的B已经不匹配了，那前面的B也一定是不匹配的，同样的情况其实还发生在第2个元素A上。

显然，发生问题的原因在于$P[j] == P[next[j]]$。

所以我们也只需要添加一个判断条件即可：

public static int[] getNext(String ps) {

    char[] p = ps.toCharArray();

    int[] next = new int[p.length];

    next[0] = -1;

    int j = 0;

    int k = -1;

    while (j < p.length - 1) {

       if (k == -1 || p[j] == p[k]) {

           if (p[++j] == p[++k]) { // 当两个字符相等时要跳过

              next[j] = next[k];

           } else {

              next[j] = k;

           }

       } else {

           k = next[k];

       }

    }

    return next;

}

好了，至此。KMP算法也结束了。

Base

算法

本文由作者按照 CC BY 4.0 进行授权