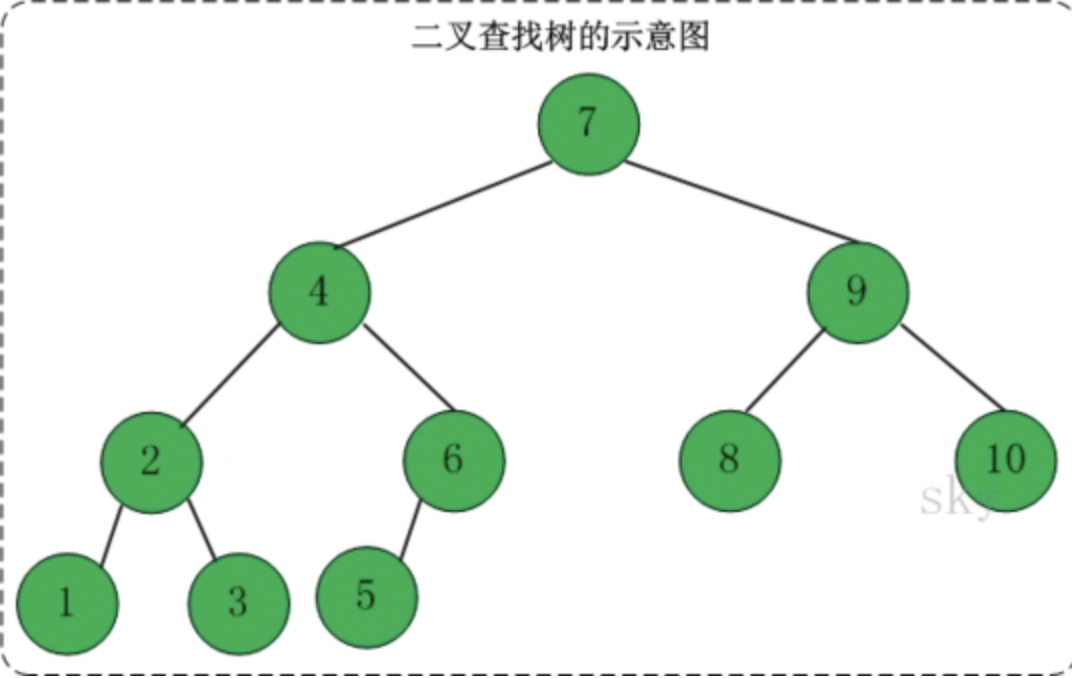
二叉查找树(Binary Search Tree),又被称为二叉搜索树。设x为二叉查找树中的一个结点,x节点包含关键字key,节点x的key值记为 $key[x]$。 如果y是x的左子树中的一个结点,则 $key[y] <= key[x]$;
如果y是x的右子树的一个结点,则 $key[y] >= key[x]$。
说明:
- 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 任意节点的左、右子树也分别为二叉查找树。
- 没有键值相等的节点(no duplicate nodes)
实现
1. 节点结构:
1
2
3
4
5
6
7
8
| typedef int Type;
typedef struct BSTreeNode{
Type key; // 关键字(键值)
struct BSTreeNode *left; // 左子树节点
struct BSTreeNode *right; // 右子树节点
struct BSTreeNode *parent; // 父结点
}Node, *BSTree;
|
2. 创建节点
1
2
3
4
5
6
7
8
9
10
11
12
13
| static Node* create_bstree_node(Type key, Node *parent, Node *left, Node* right)
{
Node* p;
if ((p = (Node *)malloc(sizeof(Node))) == NULL)
return NULL;
p->key = key;
p->left = left;
p->right = right;
p->parent = parent;
return p;
}
|
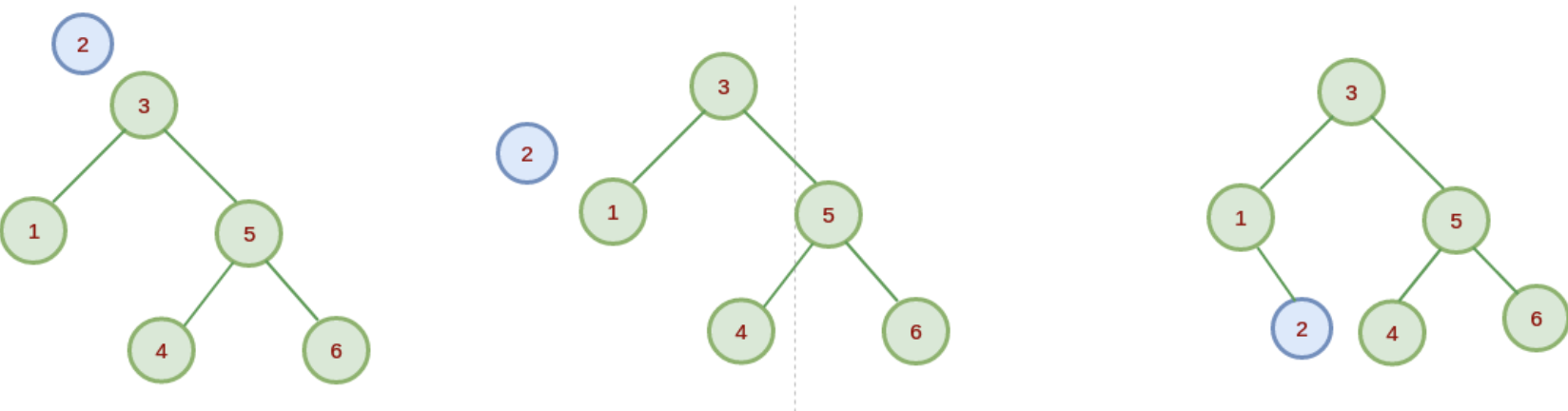
3.插入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| static Node* bstree_insert(BSTree tree, Node *z)
{
Node *y = NULL;
Node *x = tree;
// 查找z的插入位置
while (x != NULL)
{
y = x;
if (z->key < x->key)
x = x->left;
else
x = x->right;
}
z->parent = y;
if (y==NULL)
tree = z;
else if (z->key < y->key)
y->left = z;
else
y->right = z;
return tree;
}
Node* insert_bstree(BSTree tree, Type key)
{
Node *z; // 新建结点
// 如果新建结点失败,则返回。
if ((z=create_bstree_node(key, NULL, NULL, NULL)) == NULL)
return tree;
return bstree_insert(tree, z);
}
|
4. 查找
1
2
3
4
5
6
7
8
9
10
11
12
| Node* iterative_bstree_search(BSTree x, Type key)
{
while ((x!=NULL) && (x->key!=key))
{
if (key < x->key)
x = x->left;
else
x = x->right;
}
return x;
}
|
5. 最大值和最小值
1
2
3
4
5
6
7
8
9
| Node* bstree_maximum(BSTree tree)
{
if (tree == NULL)
return NULL;
while(tree->right != NULL)
tree = tree->right;
return tree;
}
|
1
2
3
4
5
6
7
8
9
| Node* bstree_minimum(BSTree tree)
{
if (tree == NULL)
return NULL;
while(tree->left != NULL)
tree = tree->left;
return tree;
}
|
6. 删除
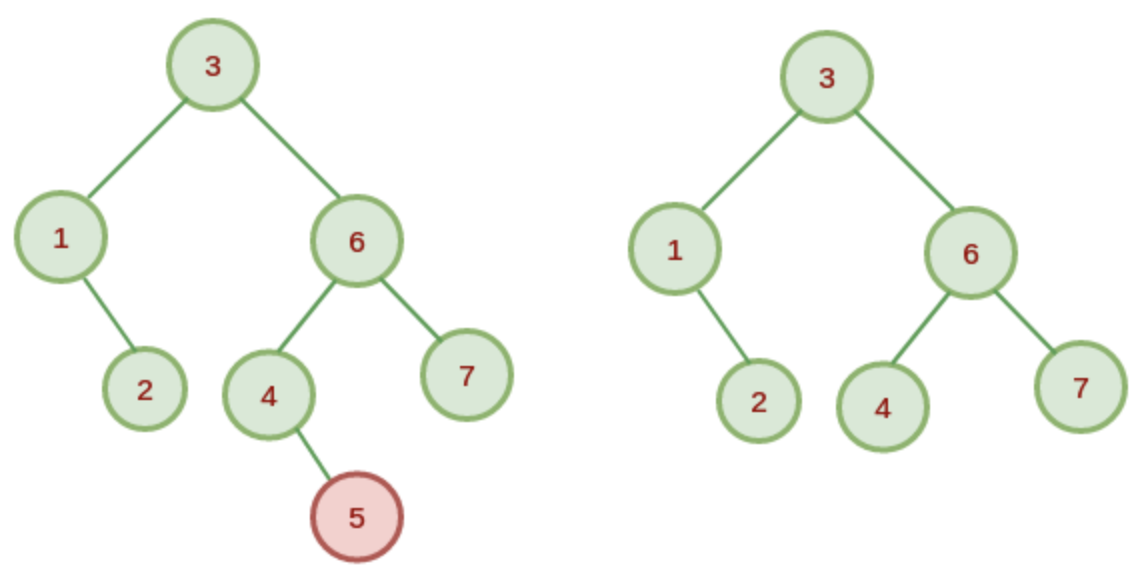
二叉查找树的删除分为三种情况:
- 删除节点为叶子节点:
直接删除叶子节点
- 删除节点只有左子树或者只有右子树:
删除节点,并将左子树或者右子树接到删除节点位置
- 删除节点左子树与右子树都有
删除节点,将左子树接到删除节点的位置,右子树接到左子树的最右子树位置。 删除节点,将右子树接到删除节点的位置,左子树接到右子树的最左子树位置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| static Node* bstree_delete(BSTree tree, Node *z)
{
Node *x=NULL;
Node *y=NULL;
if ((z->left == NULL) || (z->right == NULL) )
y = z;
else
y = bstree_successor(z);
if (y->left != NULL)
x = y->left;
else
x = y->right;
if (x != NULL)
x->parent = y->parent;
if (y->parent == NULL)
tree = x;
else if (y == y->parent->left)
y->parent->left = x;
else
y->parent->right = x;
if (y != z)
z->key = y->key;
if (y!=NULL)
free(y);
return tree;
}
Node* delete_bstree(BSTree tree, Type key)
{
Node *z, *node;
if ((z = bstree_search(tree, key)) != NULL)
tree = bstree_delete(tree, z);
return tree;
}
|
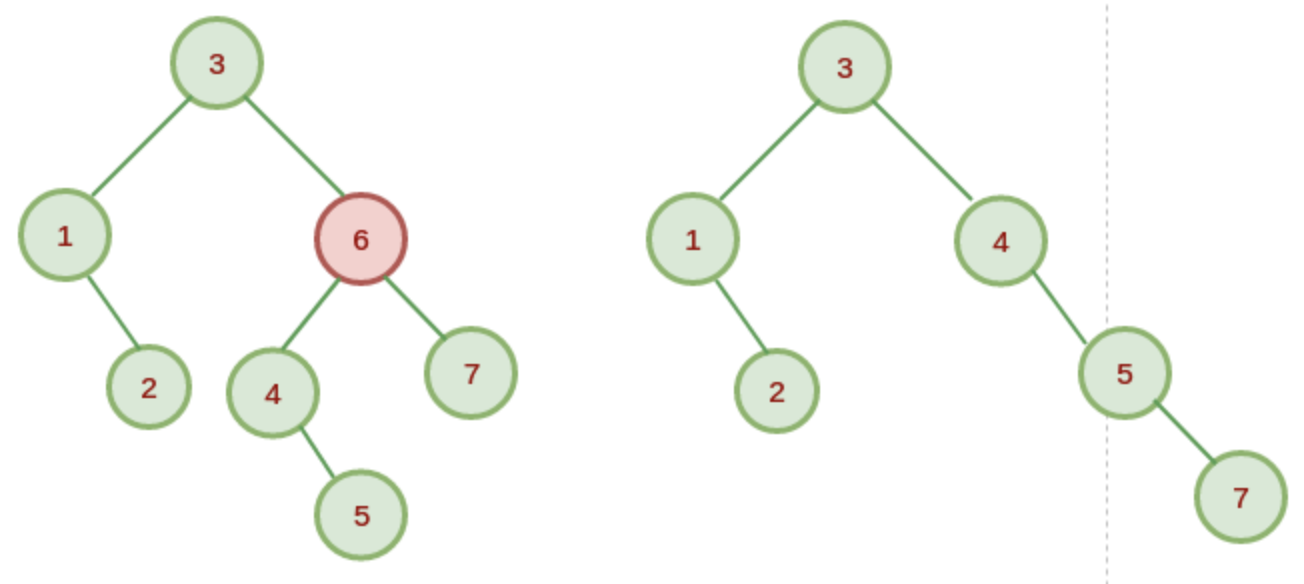 删除节点,将右子树接到删除节点的位置,左子树接到右子树的最左子树位置。
删除节点,将右子树接到删除节点的位置,左子树接到右子树的最左子树位置。