数据结构 | 二叉树的遍历

概念：

二叉树的遍历分为以下三种:

先序遍历：遍历顺序规则为【根左右】

中序遍历：遍历顺序规则为【左根右】

后序遍历：遍历顺序规则为【左右根】

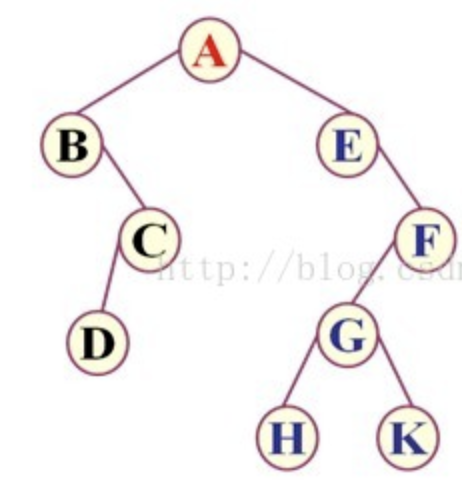
举个例子，看下图:

先序遍历：ABCDEFGHK

中序遍历：BDCAEHGKF

后序遍历：DCBHKGFEA

编程实现方式:

三种方法中，递归最为简单，栈次之，循环最为麻烦。递归的深度如果太大则会导致栈溢出；栈的方式需要额外的辅助空间；循环编程最麻烦。

1. 递归：

//递归方法  
void midPrint_r(TreeNode* root)  
{//中序遍历  
    if(root==NULL)  
        return;  
    if(root->left)  
        midPrint_r(root->left);  
    cout<<root->val<<"   ";  
    if(root->right)  
        midPrint_r(root->right);  
}  

void prePrint_r(TreeNode* root)  
{//前序遍历  
    if(root==NULL)  
        return;  
    cout<<root->val<<"   ";  
    if(root->left)  
        prePrint_r(root->left);    
    if(root->right)  
        prePrint_r(root->right);  
}  

void postPrint_r(TreeNode* root)  
{//中序遍历  
    if(root==NULL)  
        return;  
    if(root->left)  
        postPrint_r(root->left);   
    if(root->right)  
        postPrint_r(root->right);  
    cout<<root->val<<"   ";  
}

2. 栈方法：

先循环把结点压入到栈中，然后再逐个弹出；

//循环堆栈方法
void midPrint_l(TreeNode* root)
{
	stack<TreeNode*> s;
	TreeNode *cur = root;
	while(!s.empty() || cur != NULL)
	{
		while(cur != NULL)
		{
			s.push(cur);
			cur = cur->left;
		}
		cur = s.top();
		s.pop();
		cout<<cur->val<<" ";
		cur = cur->right;
	}
}

void prePrint_l(TreeNode* root)
{
	stack<TreeNode*> s;
	TreeNode *cur = root;
	while(!s.empty() || cur != NULL)
	{
		while(cur != NULL)
		{
			cout<<cur->var<<" ";
			s.push(cur);
			cur = cur->left;
		}
		cur = s.top();
		s.pop();
		cur = cur->right;
	}
}

void postPrint_l(TreeNode* root)

	if(root == NULL)
	{
		return;
	}
	stack<TreeNode*> s;
	s.push(root);
	TreeNode *cur = NULL;
	TreeNode *pre = NULL;
	while(!s.empty())
	{
		cur = s.top();
		//left down or right down
		if( pre == NULL || pre->left == cur || pre->right == cur)
		{//有左子树压左子树，有右子树压右子树，
		//都没有说明是叶子结点，直接打印并弹出
			if(cur->left != NULL)
			{//先压左子树，若左子树为空则压右子树
				s.push(cur->left);
			}
			else if(cur->right != NULL)
			{
				s.push(cur->right);
			}
			else
			{//左右子树均为空
				cout<<cur->var<<" ";
				s.pop();
			}
		}
		//left up
		else if(cur->left == pre)
		{//左边开始返回
			if(cur->right != NULL)
			{//若右孩子不为空则压入，否则，打印
				s.push(cur->right);
			}
			else
			{
				cout<<cur->var<<" ";
				s.pop();
			}
		}
		//right up
		else if(cur->right == pre)
		{//从右边返回,说明右侧已经打印完，则可以直接打印
			cout<<cur->var<<" ";
			s.pop();
		}
		pre = cur;
	}
}

循环：

利用叶子结点左右指针为空的特点，给叶子结点设置其直接后继，输出完该子结点后，再返回其直接后继；

 copy
//不用辅助空间的方式  
void midPrint_m(TreeNode *root)  
{  
    TreeNode *cur = root;  
    TreeNode *pre = NULL;  
    while(cur != NULL)  
    {  
        if(cur->left == NULL)  
        {//左孩子为空，则直接输出  
            cout<<cur->var<<" ";  
            cur = cur->right;  
        }  
        else  
        {  
            pre = cur->left;  
            while( pre->right != NULL && pre->right != cur )  
            {//找到cur的直接前驱  
                pre = pre->right;  
            }  
            if(pre->right == NULL)  
            {//设置后继结点  
                pre->right = cur;  
                cur = cur->left;  
            }  
            else  
            {  
                pre->right = NULL;//重新设置为空  
                cout<<cur->var<<" ";  
                cur = cur->right;  
            }  
        }  
    }  
}  

void prePrint_m(TreeNode *root)  
{//基本同于中遍历  
    TreeNode *cur = root;  
    TreeNode *pre = NULL;  
    while(cur != NULL)  
    {  
        if(cur->left == NULL)  
        {  
            cout<<cur->var<<" ";  
            cur = cur->right;  
        }  
        else  
        {  
            pre = cur->left;  
            while( pre->right != NULL && pre->right != cur )  
            {  
                pre = pre->right;  
            }  
            if(pre->right == NULL)  
            {  
                pre->right = cur;  
                cout<<cur->var<<" ";  
                cur = cur->left;  
            }  
            else  
            {  
                pre->right = NULL;  
                cur = cur->right;  
            }  
        }  
    }  
}  
//this is the most difficult algorithm  
void reverse_out(TreeNode *from,TreeNode *to)  
{  
    //first reverse from->to  
    //reverse  
    TreeNode *cur = from;  
    TreeNode *post = cur->right;  
    while(cur != to)  
    {  
        TreeNode *tmp = post->right;  
        post->right = cur;  
        cur = post;  
        post = tmp;  
    }  
    //already reverse,output list  
    TreeNode *traversal = cur;  
    while( cur != from )  
    {  
        cout<<cur->var<<" ";  
        cur = cur->right;  
    }  
    cout<<cur->var<<" ";  
    //reverse original  
    cur = to;  
    post = cur->right;  
    while(cur != from)  
    {  
        TreeNode *tmp = post->right;  
        post->right = cur;  
        cur = post;  
        post = tmp;  
    }  
    //restore to's right  
    to->right = NULL;  
}  
void postPrint_m(TreeNode *root)  
{  
    TreeNode *newroot = new TreeNode(0);  
    newroot->left = root;  
    newroot->right = NULL;  
    TreeNode *cur = newroot;  
    TreeNode *pre = NULL;  
    while(cur != NULL)  
    {  
        if(cur->left == NULL)  
        {  
            cur = cur->right;  
        }  
        else  
        {  
            pre = cur->left;  
            while(pre->right != NULL && pre->right != cur)  
            {  
                pre = pre->right;  
            }  
            if(pre->right == NULL)  
            {  
                pre->right = cur;  
                cur = cur->left;  
            }  
            else  
            {  
                pre->right = NULL;  
                reverse_out(cur->left,pre);  
                cur = cur->right;  
            }  
        }  
    }  
}