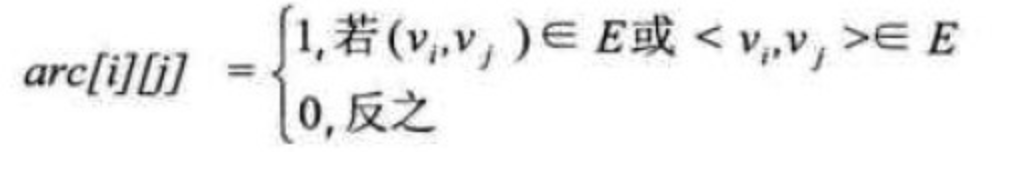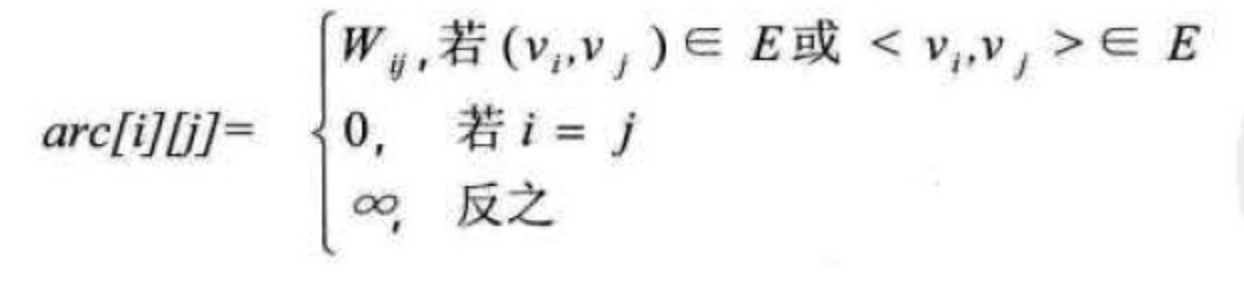数据结构 | 图的概念与存储结构
概念:
图是由顶点的有穷非空集合和顶点之间边的集合组成,通过表示为G(V,E),其中,G标示一个图,V是图G中顶点的集合,E是图G中边的集合。
无边图:若顶点$V_{i}$到$V_{j}$之间的边没有方向,则称这条边为无项边(Edge), 用序偶对$(V_{i},V_{j})$标示。
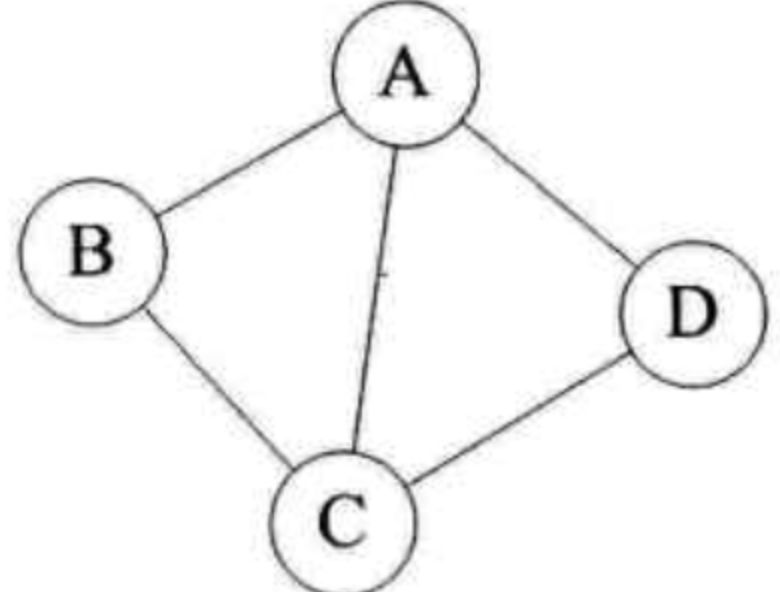
对于下图无向图G1来说,G1=(V1, {E1}),其中顶点集合V1={A,B,C,D}; 边集合E1=${(A,B),(B,C),(C,D),(D,A),(A,C)}$:
有向图:若从顶点$V_{i}$到$V_{j}$的边是有方向的,则成这条边为有向边,也称为弧(Arc)。用有序对$<V_{i},V_{j}>$标示,$V_{i}$称为弧尾,$V_{j}$称为弧头。如果任意两条边之间都是有向的,则称该图为有向图。
权(Weight):有些图的边和弧有相关的数,这个数叫做权(Weight)。这些带权的图通常称为网(Network)。
存储结构:
1.邻接矩阵(数组)表示法
图的邻接矩阵(Adjacency Matrix)存储方式是用两个数组来表示图。一个一维的数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。
设图G有n个顶点,则邻接矩阵是一个$n*n$的方阵,定义为:
我们来看一个实例,图7-4-2的左图就是一个无向图。
我们再来看一个有向图样例,如图7-4-3所示的左图。
在图的术语中,我们提到了网的概念,也就是每条边上都带有权的图叫做网。那些这些权值就需要保存下来。
设图G是网图,有n个顶点,则邻接矩阵是一个$n*n$的方阵,定义为:
如图7-4-4左图就是一个有向网图。
邻接矩阵的优点:
容易实现图的操作,如:求某顶点的度、判断顶点之间是否有边(弧)、找顶点的邻接点等等。
邻接矩阵的缺点:
n个顶点需要n*n个单元存储边(弧);空间效率为O(n^2)。 对稀疏图而言尤其浪费空间。
2. 邻接表(链式)表示法
邻接表的处理方法是这样的:
- 图中顶点用一个一维数组存储,另外,对于顶点数组中,每个数据元素还需要存储指向第一个邻接点的指针,以便于查找该顶点的边信息。
- 图中每个顶点$v_{i}$的所有邻接点构成一个线性表,由于邻接点的个数不定,所以用单链表存储,无向图称为顶点$v_{i}$的边表,有向图称为顶点$v_{i}$作为弧尾的出边表。
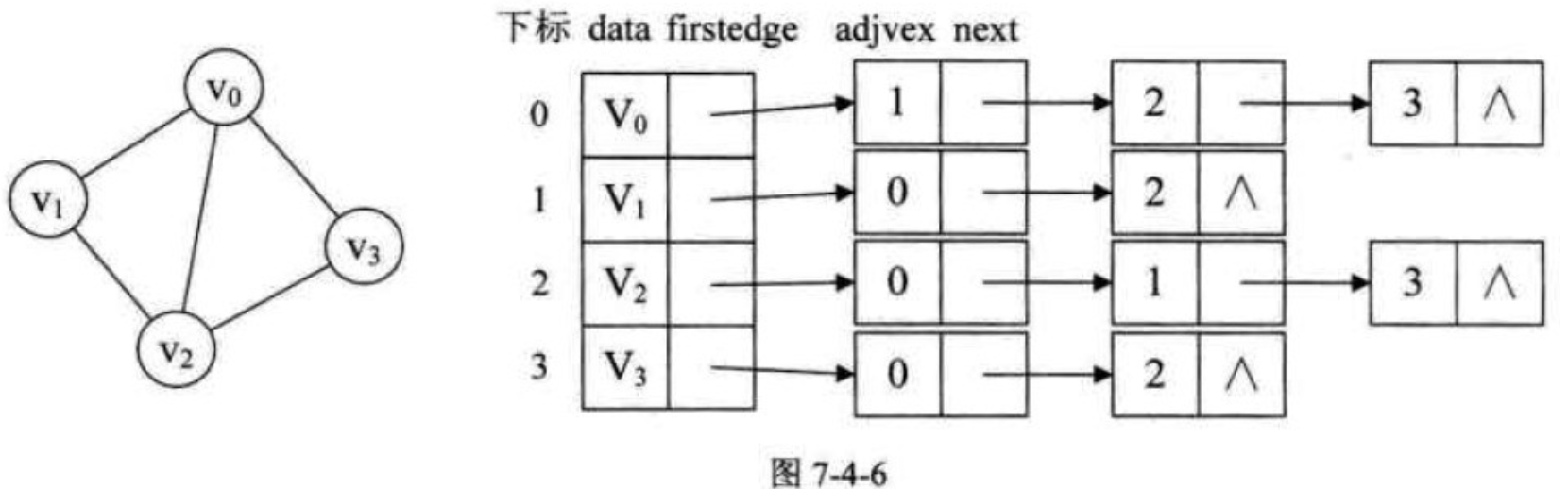
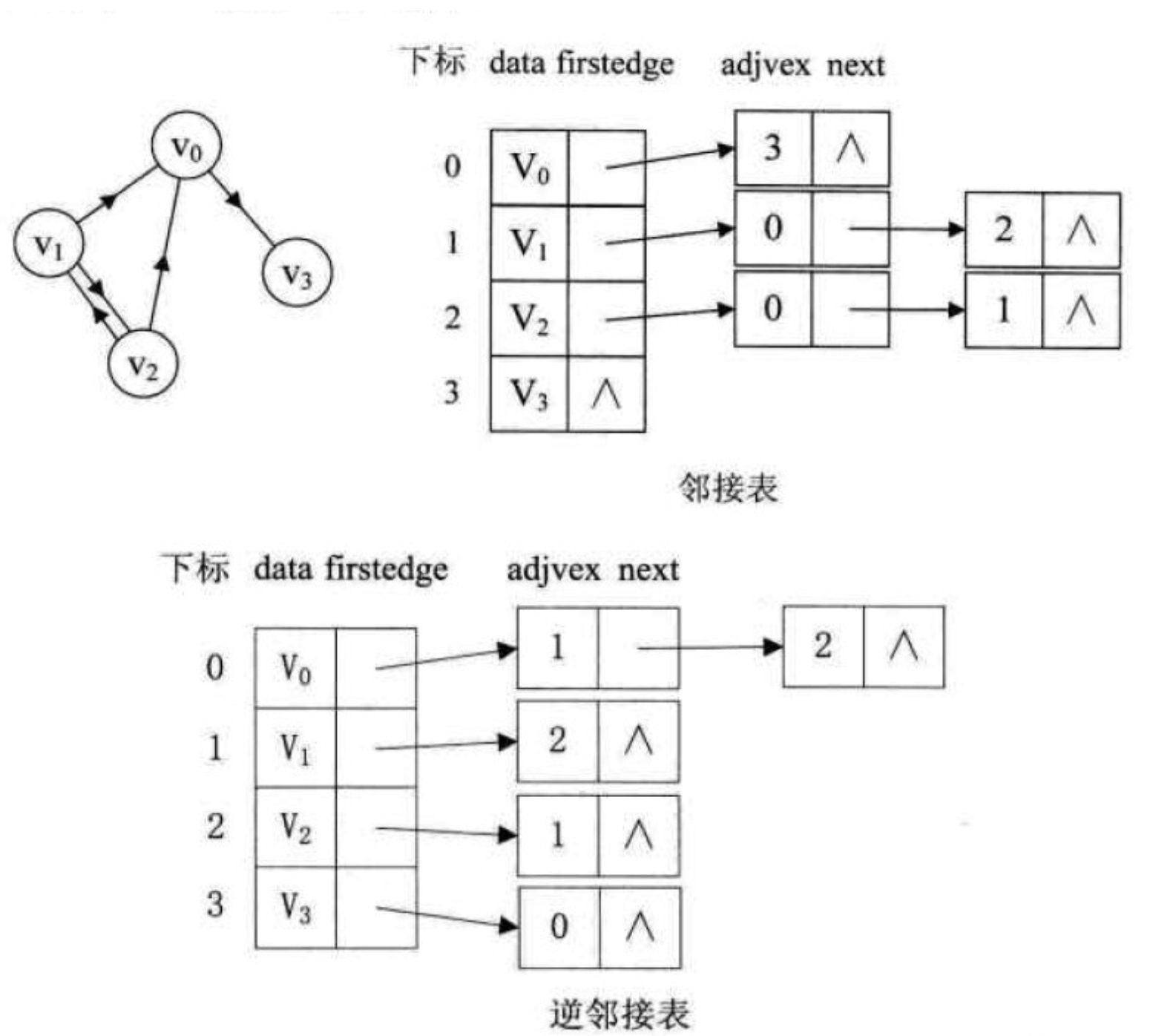
例如图7-4-6就是一个无向图的邻接表结构。
若是有向图,邻接表的结构是类似的,如图7-4-7,以顶点作为弧尾来存储边表容易得到每个顶点的出度,而以顶点为弧头的表容易得到顶点的入度,即逆邻接表。
对于带权值的网图,可以在边表结点定义中再增加一个weight的数据域,存储权值信息即可,如图7-4-8所示。
邻接表的优点:
空间效率高;容易寻找顶点的邻接点;
邻接表的缺点:
判断任意两顶点间是否有弧或边,需搜索两结点(或之一)对应的单链表,没有邻接矩阵方便。
讨论:邻接表与邻接矩阵有什么异同之处?
联系:邻接表中每个链表对应于邻接矩阵中的一行,链表中结点个数等于一行中非零元素的个数。 区别:
- 对于任一确定的图,邻接矩阵是唯一的(行列号与顶点编号一致),但邻接表不唯一(链接次序与顶点编号无关)。
- 邻接矩阵的空间复杂度为O(n^2),而邻接表的空间复杂度为O(n+e)。 用途:邻接矩阵多用于稠密图的存储(e接近 $n(n-1)/2$);而邻接表多用于稀疏图的存储($e«n^2$)
3. 十字链表(有向图的优化)
对于有向图来说,邻接表是有缺陷的。关心了出度问题,想了解入度就必须要遍历整个图才能知道。反之,逆邻接表解决了入度
却不了解出度的情况。有没有可能把邻接表和逆邻接表结合起来呢?
答案是肯定的,就是把它们整合在一起。这种存储有向图的方法是:十字链表(Orthogonal List).
我们重新定义顶点表结点结构为:
data | firstin | firstout — | — | —
firstin表示入边表头指针,指向该顶点的入边表中第一个结点, firstout表示出边表头指针,指向该顶点的出边表中的第一个结点。
重新定义的边表结点结构如下表:
tailvex | headvex | headlink | taillink — | — | — | —
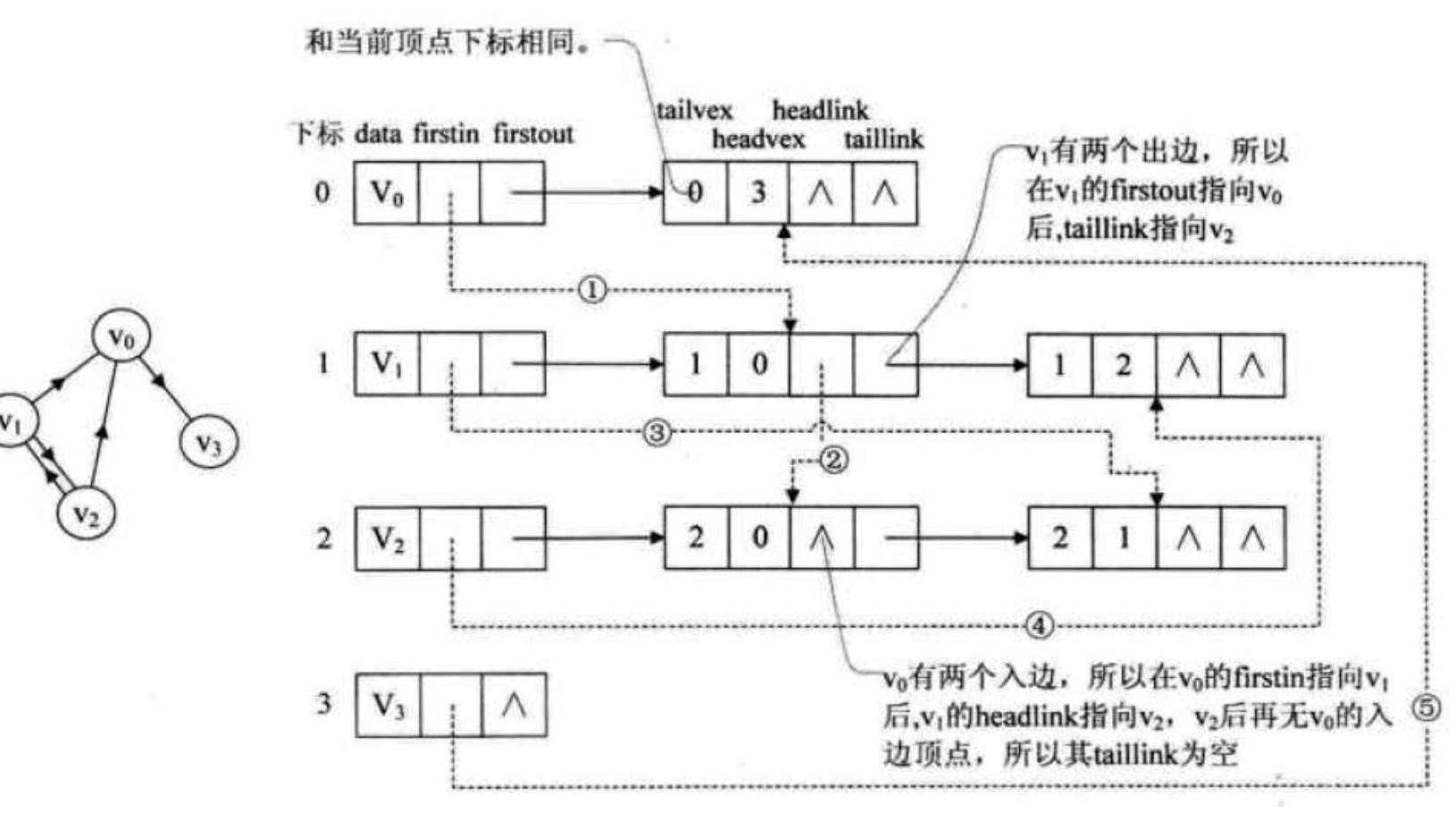
tailvex 是指弧起点在顶点表的下标, headvex 是指弧终点在顶点表中的下标, headlink 是指入边表指针域,指向终点(弧头)相同的下一条边 taillink 是指出边表指针域,指向起点(弧尾)相同的下一条边。 如果是网,还可以再增加一个weight域来存储权值。
十字链表的好处就是因为把邻接表和逆邻接表整合在了一起,这样既容易找到以vi为尾的弧,也容易找到以vi为头的弧,因而容易求得
顶点的出度和入度。除了结构复杂一点外,其实创建图算法的时间复杂度和邻接表是相同的,因此很好的应用在有向图中。
4. 邻接多重表
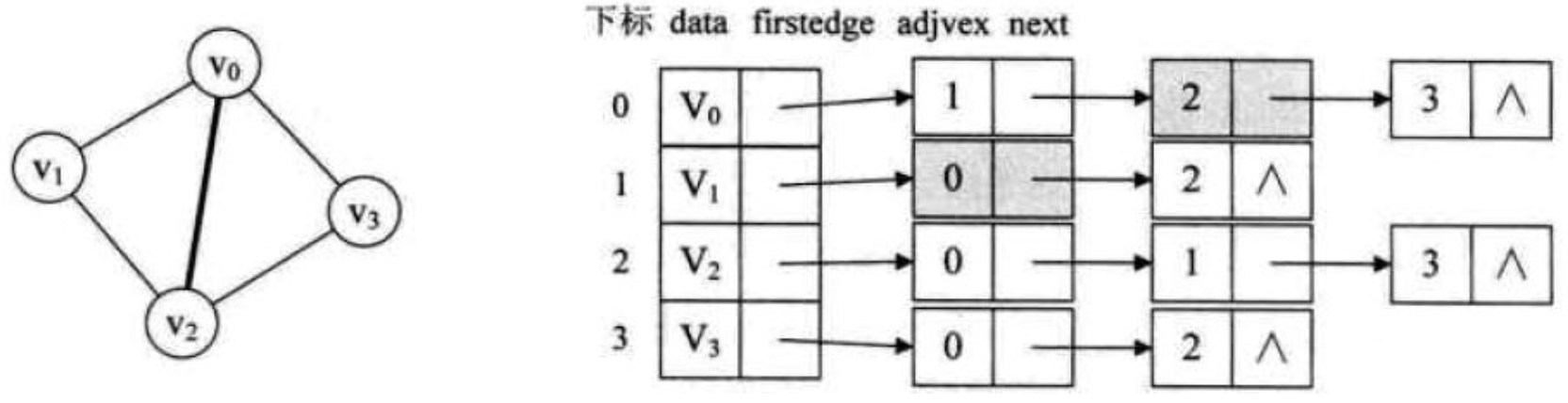
十字链表主要是针对有向图的存储结构进行了优化,那么对于无向图的邻接表,有没有问题呢? 如果我们在无向图的应用中,关注的重点是顶点,那么邻接表是不错的选择,但如果我们更关注边的操作,比如对已访问过的边做标记,删除某一条边等操作,那就意味着需要找到这条边的两个边表结点进行操作。 如下图,若要删除(v0,v2)这条边,需要对邻接表结构中右边表的两个结点进行删除,显然这是比较繁琐的。
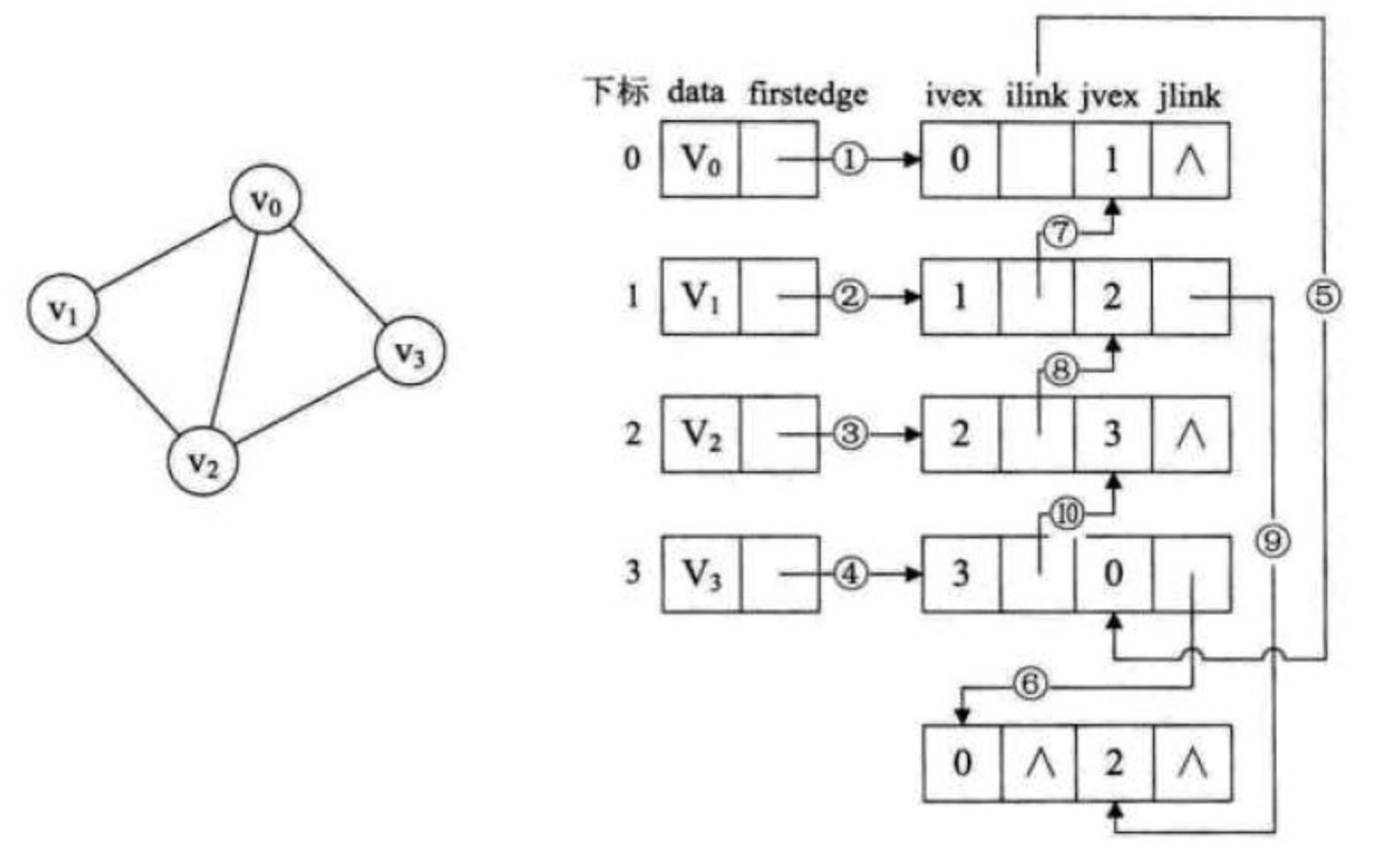
因此,我们也仿照十字链表的方式,对边表结点的结构进行一些改造,重新定义的边表结点结构如下表:
ivex | ilink | jvex | jlink — | — | — | —
ivex和jvex是指某条边依附的两个顶点在顶点表中的下标。 ilink指向依附顶点ivex的下一条边,jlink指向依附顶点jvex的下一条边。