数据结构 | 图的连通性问题之最小生成树

转载自: [勿在浮沙筑高台]

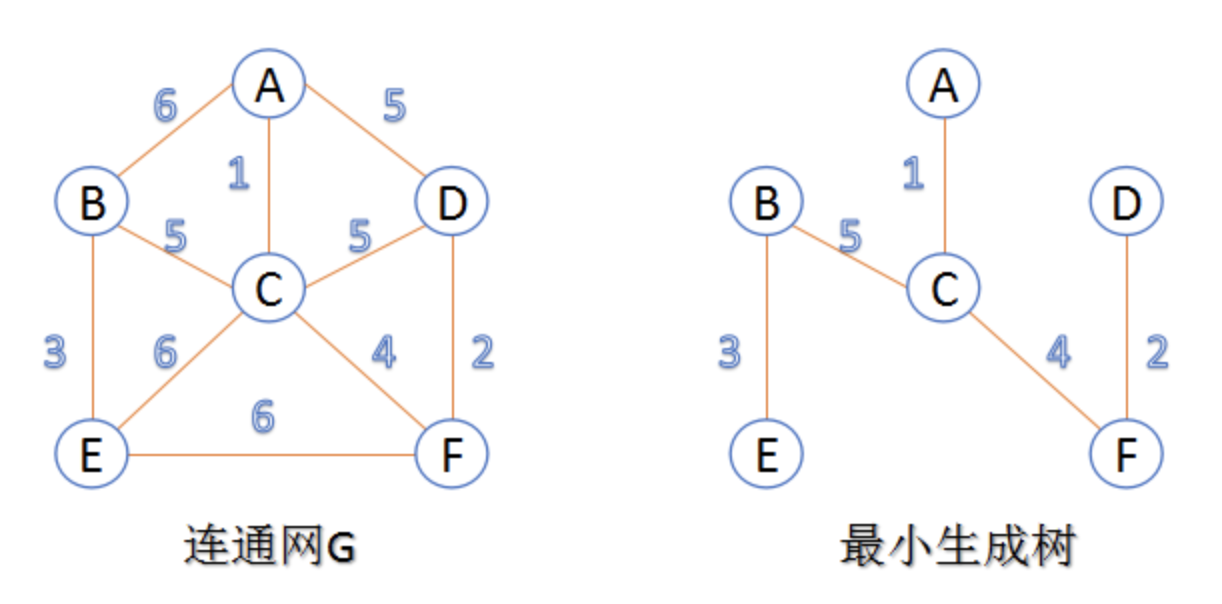
连通图：在无向图中，若任意两个顶点$v_{i}$与$v_{j}$都有路径相通，则称该无向图为连通图。 强连通图：在有向图中，若任意两个顶点$v_{i}$与$v_{j}都有路径相通，则称该有向图为强连通图。 连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。 生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。 最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

---

Kruskal算法：

此算法可以称为 “加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。

1. 把图中的所有边按代价从小到大排序；
2. 把图中的n个顶点看成独立的n棵树组成的森林；
3. 按权值从小到大选择边，所选的边连接的两个顶点$(u_{i},v_{i}$,应属于两颗不同的树，则成为最小生成树的一条边，并将这两颗树合并作为一颗树。
4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。

typedef struct          
{        
    char vertex[VertexNum];                                //顶点表         
    int edges[VertexNum][VertexNum];                       //邻接矩阵,可看做边表         
    int n,e;                                               //图中当前的顶点数和边数         
}MGraph;

typedef struct node  
{  
    int u;                                                 //边的起始顶点   
    int v;                                                 //边的终止顶点   
    int w;                                                 //边的权值   
}Edge;

void kruskal(MGraph G)  
{  
    int i,j,u1,v1,sn1,sn2,k;  
    int vset[VertexNum];                                    //辅助数组，判定两个顶点是否连通   
    int E[EdgeNum];                                         //存放所有的边   
    k=0;                                                    //E数组的下标从0开始  

    // 初始化所有边信息， 构造数组
    for (i=0;i<G.n;i++)  
    {  
        for (j=0;j<G.n;j++)  
        {  
            if (G.edges[i][j]!=0 && G.edges[i][j]!=INF)  
            {  
                E[k].u=i;  
                E[k].v=j;  
                E[k].w=G.edges[i][j];  
                k++;  
            }  
        }  
    }     
    heapsort(E,k,sizeof(E[0]));                            //堆排序，按权值从小到大排列边

    for (i=0;i<G.n;i++)                                    //初始化辅助数组   
    {  
        vset[i]=i;  
    }  

    k=1;                                                   //生成的边数，最后要刚好为总边数   
    j=0;                                                   //E中的下标   

    while (k<G.n)  
    {   
        sn1=vset[E[j].u];  
        sn2=vset[E[j].v];                                  //得到两顶点属于的集合编号  

        if (sn1!=sn2)                                      //不在同一集合编号内的话，把边加入最小生成树  ------- 重点过程
        {
            printf("%d ---> %d, %d",E[j].u,E[j].v,E[j].w);       
            k++;  
            for (i=0;i<G.n;i++)   // 遍历所有的节点
            {
                if (vset[i]==sn2)  
                {  
                    vset[i]=sn1;  
                }  
            }             
        }  
        j++;  
    }  
}

---

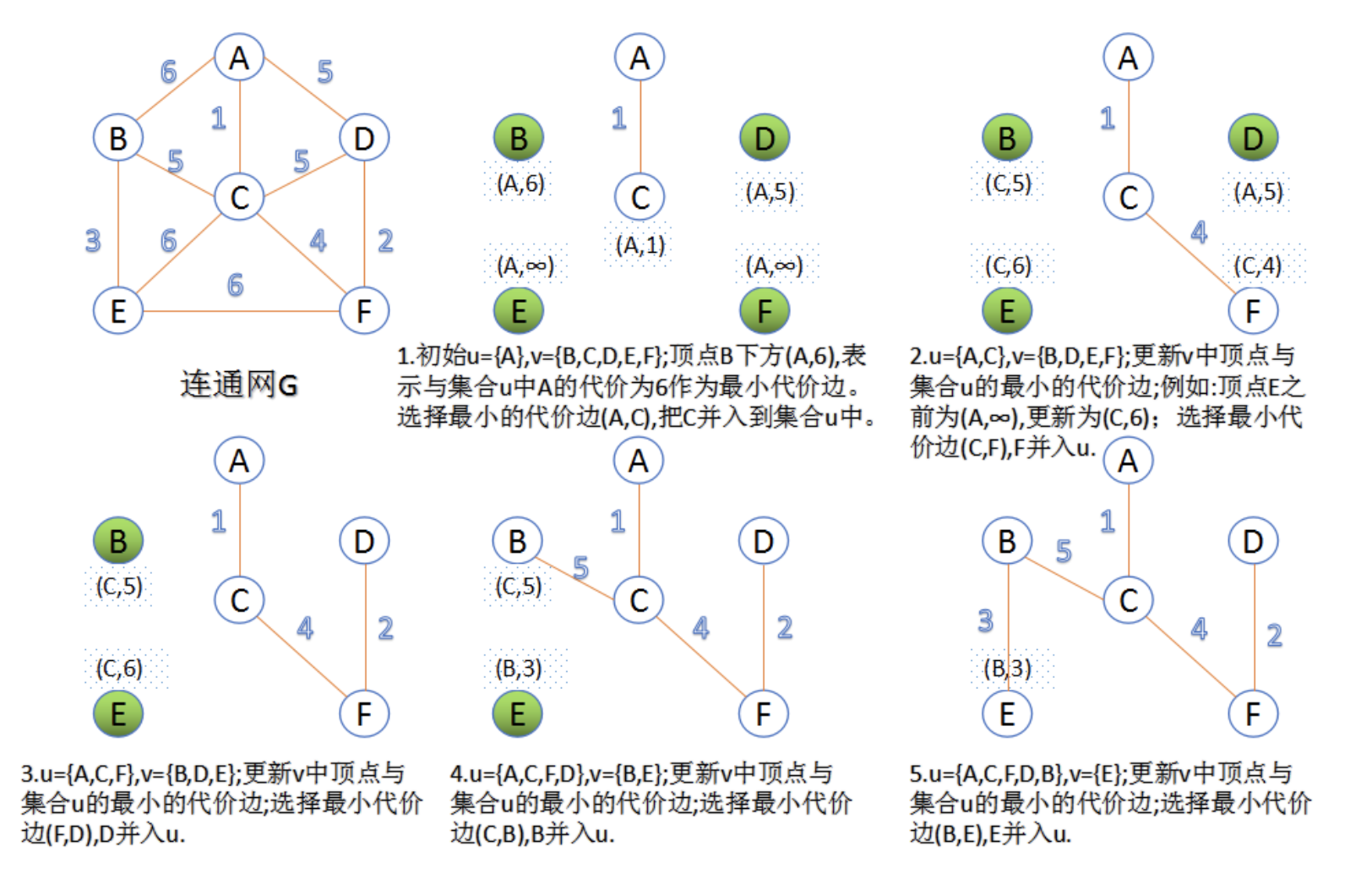
Prim算法

此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。

算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

1. 图的所有顶点集合为$V$；初始令集合$u={s},v=V-u$;
2. 在两个集合$(u,v)$能够组成的边中，选择一条代价最小的边$(u_0,v_0)$，加入到最小生成树中，并把$v0$并入到集合u中。
3. 重复上述步骤，直到最小生成树有n-1条边或者n个顶点为止。

由于不断向集合u中加点，所以最小代价边必须同步更新；需要建立一个辅助数组closedge,用来维护集合v中每个顶点与集合u中最小代价边信息，

struct
{
  char vertexData   //表示u中顶点信息
  UINT lowestcost   //最小代价
}closedge[vexCounts]

#define MAX  100000
#define VNUM  10+1                                             //这里没有ID为0的点,so id号范围1~10

int edge[VNUM][VNUM]={/*输入的邻接矩阵*/};
int lowcost[VNUM]={0};                                         //记录Vnew中每个点到V中邻接点的最短边
int addvnew[VNUM];                                             //标记某点是否加入Vnew
int adjecent[VNUM]={0};                                        //记录V中与Vnew最邻近的点


void prim(int start)
{
     int sumweight=0;
     int i,j,k=0;

     for(i=1;i<VNUM;i++)                                      //顶点是从1开始
     {
        lowcost[i]=edge[start][i];
        addvnew[i]=-1;                                         //将所有点至于Vnew之外,V之内，这里只要对应的为-1，就表示在Vnew之外
     }

     addvnew[start]=0;                                        //将起始点start加入Vnew
     adjecent[start]=start;

     for(i=1;i<VNUM-1;i++)                                        
     {
        int min=MAX;
        int v=-1;
        for(j=1;j<VNUM;j++)                                      
        {
            if(addvnew[j]!=-1&&lowcost[j]<min)                 //在Vnew之外寻找最短路径
            {
                min=lowcost[j];
                v=j;
            }
        }
        if(v!=-1)
        {
            printf("%d %d %d\n",adjecent[v],v,lowcost[v]);
            addvnew[v]=0;                                      //将v加Vnew中

            sumweight+=lowcost[v];                             //计算路径长度之和
            for(j=1;j<VNUM;j++)
            {
                if(addvnew[j]==-1&&edge[v][j]<lowcost[j])      
                {
                    lowcost[j]=edge[v][j];                     //此时v点加入Vnew 需要更新lowcost
                    adjecent[j]=v;                             
                }
            }
        }
    }
    printf("the minmum weight is %d",sumweight);
}