数据结构 | 排序问题之选择排序
1. 简单选择排序
选择排序(Selection Sort)是一种简单直观的排序算法。
它的工作原理如下: 首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。 以此类推,直到所有元素均排序完毕。
选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上,则它不会被移动。 选择排序每次交换一对元素,它们当中至少有一个将被移到其最终位置上,因此对n个元素的序列进行排序总共进行至多n-1次交换。在所有的完全依靠交换去移动元素的排序方法中,选择排序属于非常好的一种。
实例分析
以数组 arr=[8, 5, 2, 6, 9, 3, 1, 4, 0, 7] 为例,先直观看一下每一步的变化,后面再介绍细节
第一次从数组 [8, 5, 2, 6, 9, 3, 1, 4, 0, 7] 中找到最小的数 0,放到数组的最前面(与第一个元素进行交换)
1
2
3
4
5
min ↓
8 5 2 6 9 3 1 4 0 7
↑ ↑
└───────────────────────────────┘
交换后:
1
0 5 2 6 9 3 1 4 8 7
在剩余的序列中 [5, 2, 6, 9, 3, 1, 4, 8, 7] 中找到最小的数 1,与该序列的第一个个元素进行位置交换:
1
2
3
4
5
min
↓
0 5 2 6 9 3 1 4 8 7
↑ ↑
└───────────────────┘
交换后:
1
0 1 2 6 9 3 5 4 8 7
在剩余的序列中 [2, 6, 9, 3, 5, 4, 8, 7] 中找到最小的数 2,与该序列的第一个个元素进行位置交换(实际上不需要交换):
1
2
3
4
min
↓
0 1 2 6 9 3 5 4 8 7
↑
重复上述过程,直到最后一个元素就完成了排序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
min
↓
0 1 2 6 9 3 5 4 8 7
↑ ↑
└───────┘
min
↓
0 1 2 3 9 6 5 4 8 7
↑ ↑
└───────────┘
min
↓
0 1 2 3 4 6 5 9 8 7
↑ ↑
└───┘
min
↓
0 1 2 3 4 5 6 9 8 7
↑
min
↓
0 1 2 3 4 5 6 9 8 7
↑ ↑
└───────┘
min
↓
0 1 2 3 4 5 6 7 8 9
↑
min
↓
0 1 2 3 4 5 6 7 8 9
↑
代码分析:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <iostream>
using namespace std;
void SelectSort(int *pData,int size)
{
for(int i = 0;i<size-1;++i)
{
int index = i;
for(int j = i+1;j<size;++j)
{
if(pData[j]<pData[index])
index = j;
}
if(index != i)
{
int temp = pData[i];
pData[i] = pData[index];
pData[index] = temp;
}
}
}
int main()
{
int pData[10]={1,5,9,3,4,7,8,2,6,10};
for(int i = 0;i<10;++i)
cout<<pData[i]<<' ';
cout<<endl;
SelectSort(pData,10);
for(int i = 0;i<10;++i)
cout<<pData[i]<<' ';
return 0;
}
2. 堆排序
作为选择排序的改进版,堆排序可以把每一趟元素的比较结果保存下来,以便我们在选择最小/大元素时对已经比较过的元素做出相应的调整。
堆排序是一种树形选择排序,在排序过程中可以把元素看成是一颗完全二叉树,每个节点都大(小)于它的两个子节点
当每个节点都大于等于它的两个子节点时,就称为大顶堆,也叫堆有序; 当每个节点都小于等于它的两个子节点时,就称为小顶堆。
算法思想(以大顶堆为例):
- 将长度为n的待排序的数组进行堆有序化构造成一个大顶堆
- 将根节点与尾节点交换并输出此时的尾节点
- 将剩余的n -1个节点重新进行堆有序化
- 重复步骤2,步骤3直至构造成一个有序序列
举例:
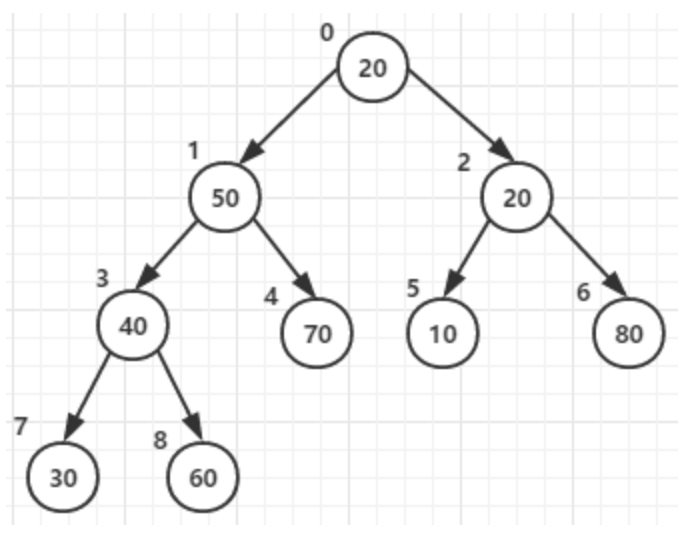
假设待排序数组为[20,50,10,30,70,20,80]
构造堆:
在构造有序堆时,我们开始只需要扫描一半的元素(n/2-1 ~ 0)即可,为什么? 因为(n/2-1)~0的节点才有子节点,如图1,n=8,(n/2-1) = 3 即3 2 1 0这个四个节点才有子节点
所以接下来就是将3 2 1 0这四个节点从下到上,从右到左的与它自己的子节点比较并调整最终形成大顶堆,过程如下:
第一次for循环将节点3和它的子节点7 8的元素进行比较,最大者作为父节点(即元素60作为父节点)
[红色表示交换后的状态]
接下来将节点2和它的子节点5 6的元素进行比较,最大者为父节点(元素80作为父节点)
然后将节点1和它的子节点3 4的元素进行比较,最大者为父节点(元素70作为父节点)
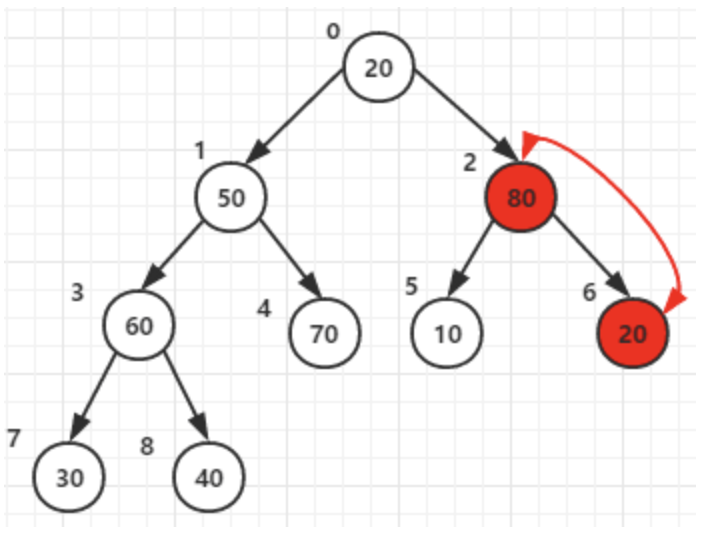
最后将节点0和它的子节点1 2的元素进行比较,最大者为父节点(元素80作为父节点)
至此有序堆已经构造好了!如下图:
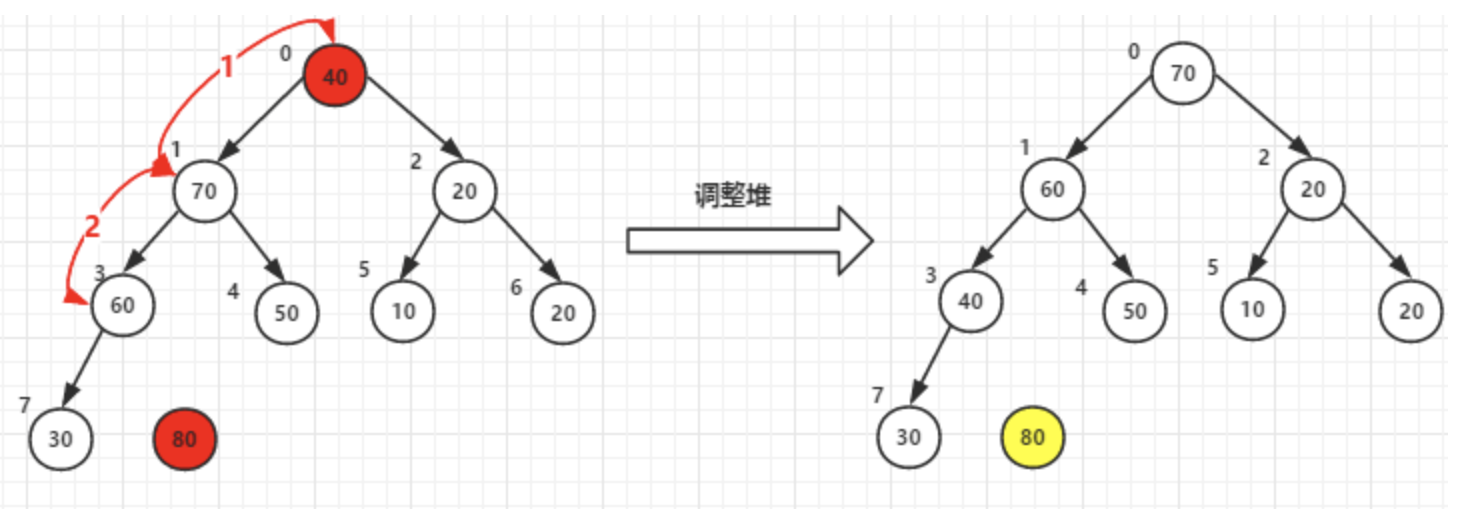
调整堆
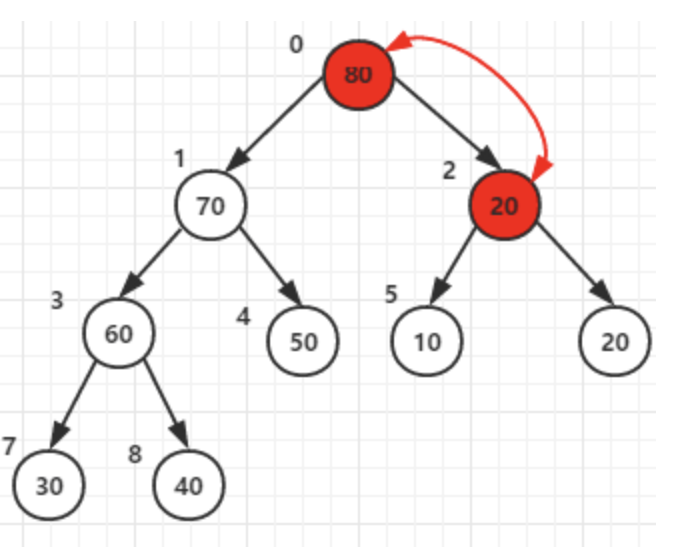
1)堆顶元素80和尾40交换后–>调整堆
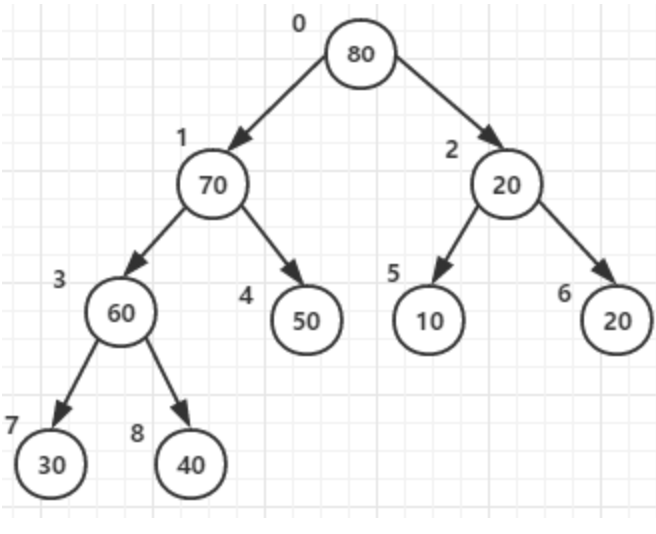
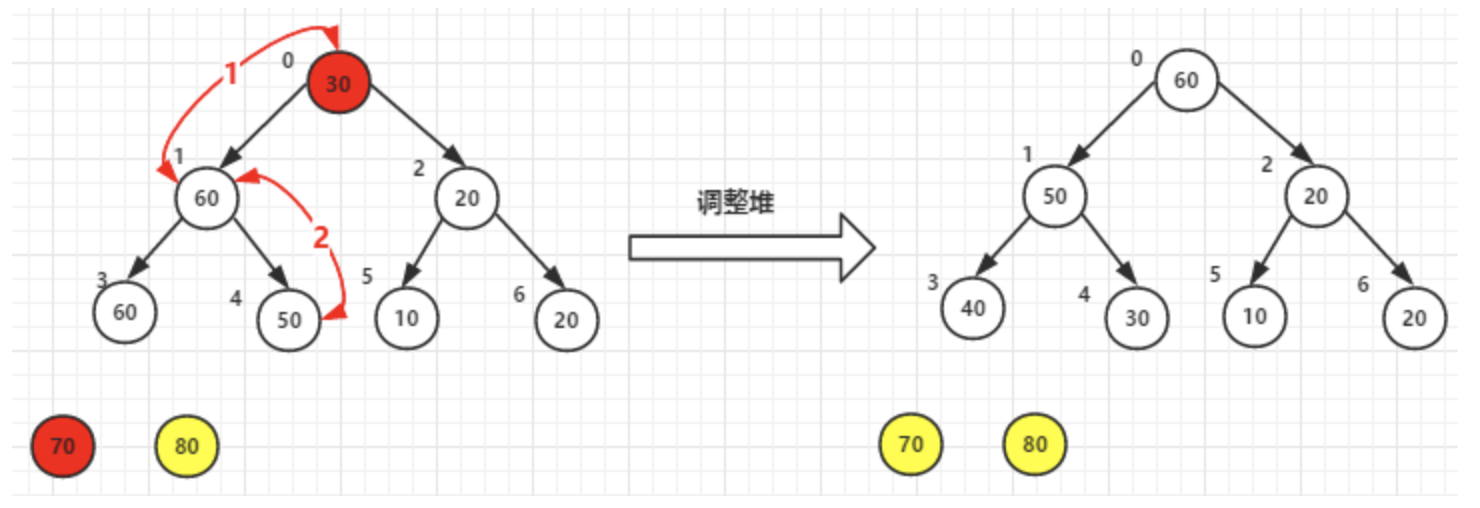
2)堆顶元素70和尾30交换后–>调整堆
4)其他依次类推,最终已排好序的元素如下:
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
public class HeapSort {
private static void heapSort(int[] arr) {
int len = arr.length -1;
for(int i = len/2 - 1; i >=0; i --){ //堆构造
heapAdjust(arr,i,len);
}
while (len >=0){
swap(arr,0,len--); //将堆顶元素与尾节点交换后,长度减1,尾元素最大
heapAdjust(arr,0,len); //再次对堆进行调整
}
}
public static void heapAdjust(int[] arr,int i,int len){
int left,right,j ;
while((left = 2*i+1) <= len){ //判断当前父节点有无左节点(即有无孩子节点,left为左节点)
right = left + 1; //右节点
j = left; //j"指针指向左节点"
if(j < len && arr[left] < arr[right]) //右节点大于左节点
j ++; //当前把"指针"指向右节点
if(arr[i] < arr[j]) //将父节点与孩子节点交换(如果上面if为真,则arr[j]为右节点,如果为假arr[j]则为左节点)
swap(arr,i,j);
else //说明比孩子节点都大,直接跳出循环语句
break;
i = j;
}
}
public static void swap(int[] arr,int i,int len){
int temp = arr[i];
arr[i] = arr[len];
arr[len] = temp;
}
public static void main(String[] args) {
int array[] = {20,50,20,40,70,10,80,30,60};
System.out.println("排序之前:");
for(int element : array){
System.out.print(element+" ");
}
heapSort(array);
System.out.println("\n排序之后:");
for(int element : array){
System.out.print(element+" ");
}
}
}