机器学习篇 | BP 神经网络引入
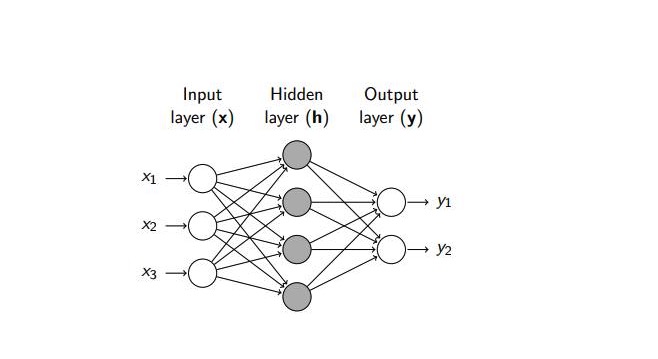
BP 神经网络是指使用BP算法训练的前馈神经网络, 神经网络模型形如:
神经网络基本分位三部分 :
- 输入层对接样本的特征向量
- 中间包含0到多个隐含层
- 输出层对应预测结果
神经网络中的每一个神经节点都是一个神经元
常见的激活函数有sigmod, ReLU, tanh
单层神经网络主要用来解决线性可分的问题, 对于不可分的问题, 采用多层神经网络
BP 神经网络训练与预测
给定训练集 $D= \lbrace (x_1, y_1),(x_2, y_2), …, (x_m, y_m) \rbrace , x_i \in \mathbb{R}^{d}, y_i \in \mathbb{R}^{l}$ , 即输入的样本有 $d$ 个特征值, 输出 $l$ 为实值向量。 在上面模型中, 我们定义了具有 $q$ 个神经元的单隐层, 在每层添加一个值为 $1$ 的常量来起到阈值的作用,这样就可以将阈值放进权重矩阵内部。
所以就有隐层第 $h$ 个神经元接受到的输入为 $\alpha_h = \sum_{i=1}^{d+1}v_{ih}x_{i}, x_{d+1}=1$, 输出层第 $j$ 个神经元接受到的输入为 $\beta_j = \sum_{h=1}^{q+1} w_{hj}b_h, b_{q+1}=1$
对于激活函数我们采用 sigmod, 损失函数采用均方差。
对于样本 $(x_k, y_k)$ , 均方差为 :
\[E^{k}_{j} = \frac{1}{2} \sum_{j=1}{l} (\hat{y}^{k}_{j} - y^{k}_{j})^2\]链式求导法则 :
第二层权重计算:
\[\frac{\partial E^{k}}{\partial w_{hj}} = \frac{\partial E^{k}_{j}}{\partial \hat{y}^{k}_{j}} \cdot \frac{\partial \hat{y}^{k}_{j}}{\partial \beta_{j}} \cdot \frac{\partial \beta_j}{\partial w_{hj}}\]第一层权重计算
\[\frac{\partial E^{k}}{\partial v_{ih}} = \sum_{j=1}^{l} \frac{\partial E_{j}^{k}}{\partial b_h} \cdot \frac{\partial b_h}{\partial \alpha_h } \cdot \frac{ \partial \alpha_h }{ \partial v_{ih} }\] \[\frac{\partial E_{j}^{k}}{\partial b_h} = \frac{\partial E^{k}_{j}}{\partial \hat{y}^{k}_{j}} \cdot \frac{\partial \hat{y}^{k}_{j}}{\partial \beta_{j}} \cdot \frac{\partial \beta_j}{\partial b_h}\]对于 均方差损失函数 :
\[\frac{ \partial E^{k} }{ \partial \hat{y}^{k}_{j} } = \hat{y}^{k}_{j} - y^{k}\]对于 sigmod 激活函数 :
\[f \prime (x) = f(x)(1-f(x))\]所以有 :
\[\frac{\partial \hat{y}^{k}_{j}}{\partial \beta_{j}} = \hat{y}^{k}_{j}(1-\hat{y}^{k}_{j})\] \[\frac{ \partial b_h }{ \partial \alpha_h } = b_{h} (1-b_{h})\]引入 :
\[g_{j} = \frac{ \partial E^{k}_{j} }{ \partial \hat{y}^{k}_{j} } \cdot \frac{ \partial \hat{y}^{k}_{j} }{ \partial \beta_{j} } = \hat{y}^{k}_{j}(1-\hat{y}^{k}_{j})(\hat{y}^{k}_{j} - y^{k})\]则有
\[\frac{\partial E^{k}}{\partial w_{hj}} = g_{j}b_h\] \[\frac{\partial E^{k}}{\partial v_{ih}} = b_{h} (1-b_{h}) x_i \sum_{j=1}^{l} g_{j} w_{hj}\]累计误差
累计误差在读取整个训练集D一遍后才进行更新,参数更新频率低
\[E=\frac{1}{m} \sum_{k=1}^{m} E_k\]代码样例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
####
# BP 算法与前馈神经网络
#
# X 维度 : 13 + 1
# 隐藏层 : 10 + 1
# 输出层 : 3
# 权重矩阵 V : 14 * 10
# 权重矩阵 W : 11 * 3
##
from sklearn.datasets import load_iris
from sklearn.datasets import load_wine
from sklearn.decomposition import PCA
from sklearn.preprocessing import OneHotEncoder
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pylab as plt
def draw_data(X, Y):
plt.scatter(X[:,0], X[:,1], c=Y)
plt.show()
def active_func(z) -> np :
"""
定义激活函数 -- sigmod
:param z:
:return:
"""
return 1 / (1 + np.e ** (-z))
def err_sample(y_hat:np, y:np) -> int :
"""
比较错误情况
:param y_hat:
:param y:
:return:
"""
hat_max = np.argmax(y_hat, axis=0)
y_max = np.argmax(y, axis=0)
success_y = y_max[y_max == hat_max]
return len(y_max) - len(success_y)
def model(X:np, Y:np):
"""
模型训练
:param X:
:param Y:
:return:
"""
n_feture = X.shape[0]
n_hide = 25
n_out = Y.shape[0]
# 初始化权重矩阵
v_matrix = np.random.randn(n_hide, n_feture+1)
w_matrix = np.random.randn(n_out, n_hide+1)
# 学习率
alpha = 0.007
n_sample = X.shape[1]
step = 5
itera = 5000
for iter_i in range(itera) :
err_count = 0
for i in range(int(n_sample/step)) :
min_sample_index = i * step
max_sample_index= min((i+1) * step, n_sample)
sample_size = max_sample_index - min_sample_index
sample_x = X[:, min_sample_index:max_sample_index]
sample_y = Y[:, min_sample_index:max_sample_index]
# # 计算隐层
x_bias = np.linspace(1, 1, sample_size)
sample_x = np.row_stack((sample_x, x_bias))
B = active_func(np.dot(v_matrix, sample_x))
# 计算输出层
b_bias = np.linspace(1,1 , sample_size)
B = np.row_stack((B, b_bias))
sample_y_hat = active_func(np.dot(w_matrix, B))
# 累计错误样本数
err_count = err_count + err_sample(sample_y_hat, sample_y)
# 使用平方损失函数 --- 梯度下降法
# 计算 w 的梯度
w_matrix_grad = np.dot((sample_y_hat - sample_y) * sample_y_hat * (1- sample_y_hat), B.T) / sample_size
# 计算 v 的梯度
v_matrix_grad = np.dot((np.dot(((sample_y_hat - sample_y) * sample_y_hat * (1-sample_y_hat)).T, w_matrix).T * (B * 1-B))[:-1,:], sample_x.T) / sample_size
# 更新梯度
w_matrix = w_matrix - alpha * w_matrix_grad
v_matrix = v_matrix - alpha * v_matrix_grad
print("{0} iter error ratio : {1}".format(iter_i, err_count/n_sample))
return w_matrix, v_matrix
def test_data(x:np, y:np, w_matrix, v_matrix) :
"""
测试模型的准确率
:param x:
:param y:
:param w_matric:
:param v_matric:
:return:
"""
n_sample = x.shape[1]
x_bias = np.linspace(1, 1, n_sample)
x = np.row_stack((x, x_bias))
B = active_func(np.dot(v_matrix, x))
# 计算输出层
b_bias = np.linspace(1, 1, n_sample)
B = np.row_stack((B, b_bias))
y_hat = active_func(np.dot(w_matrix, B))
error_count = err_sample(y_hat, y)
print("test sample error ratio : {0}".format(error_count/n_sample))
if __name__ == '__main__':
wine_data = load_iris()
X = wine_data.data
Y = wine_data.target
X = X
Y = OneHotEncoder().fit_transform(Y.reshape(-1,1)).toarray()
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.2)
w_matrix, v_matrix = model(x_train.T, y_train.T)
test_data(x_test.T, y_test.T, w_matrix, v_matrix)
说明
- 代码采用特征为连续属性莺尾花样本集
- 参考 [周志华-机器学习]
本文由作者按照 CC BY 4.0 进行授权