机器学习篇 | 支持向量机svm

引入

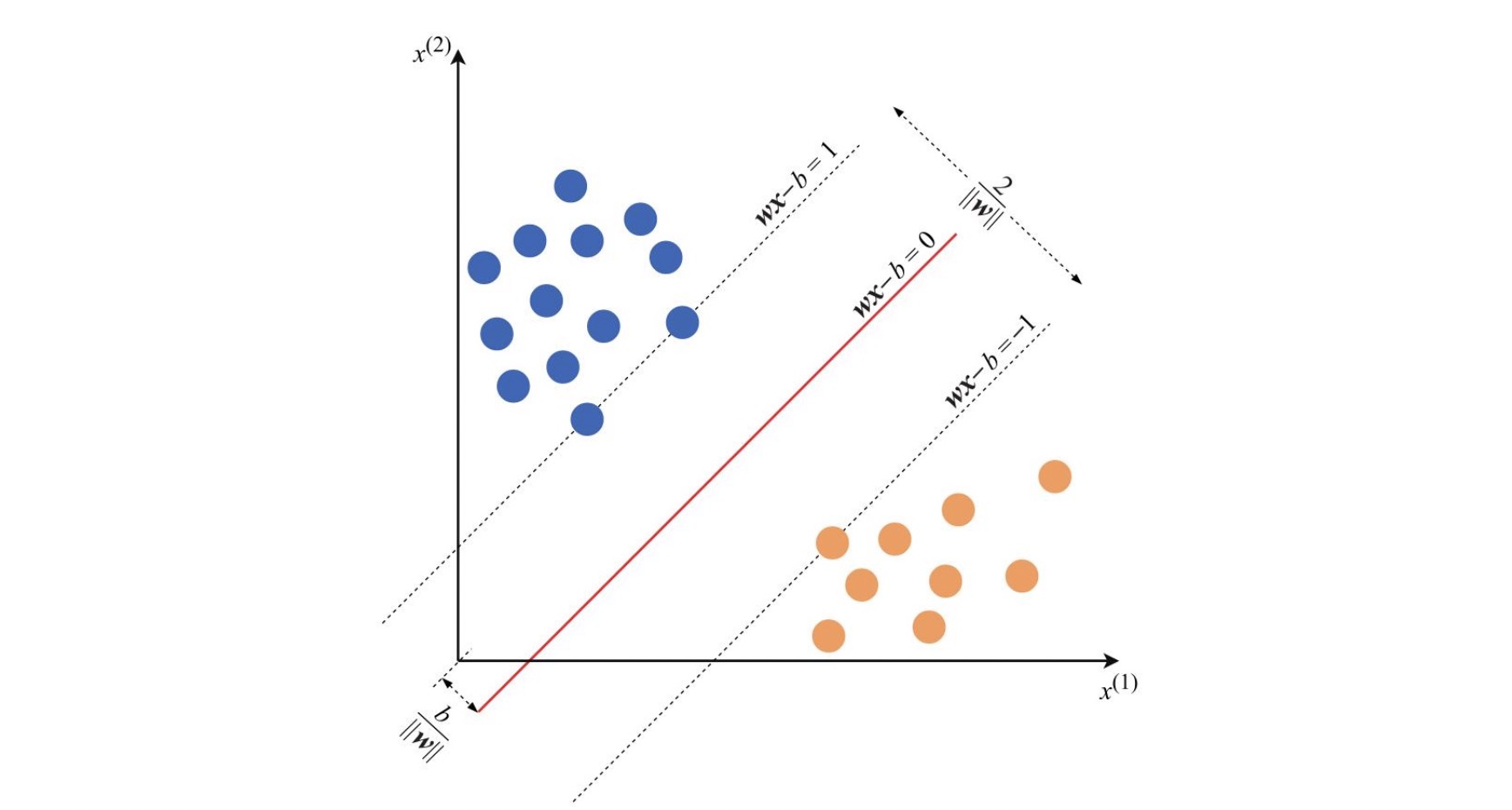
svm 解决二分类问题, 对于样本的向量空间分布集, svm 旨在要寻找一个分割面，将样本集按照分类标签正确的分割开来。我们称这个分割平面为分离超平面。

假设空间样本集是可分割的， 那么总存在无数个超平面可以将样本集分割， 如何才能找到一个最优的超平面？

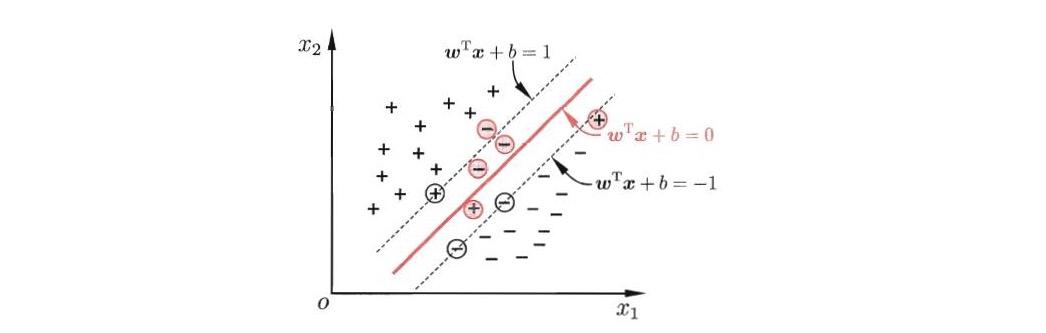
svm 的目标是找一个最优超平面，使得距离超平面最近的点的间隔距离最大化。 这个距离超平面最近的点就是支持向量。

首先定义特征空间的训练样本集 : $T=\lbrace (x_1, y_1), (x_2, y_2), …, (x_N, y_N) \rbrace$

其中， $x_i \in \mathbb{R}^{n}, y_{i} \in \lbrace -1, 1 \rbrace, i = 1, 2, …, N$ , $x_i$ 为第 $i$ 个特征向量， $y_i$ 为类标记，当它等于 $+1$ 时为正例；为 $-1$ 为负例。再假设训练数据集是线性可分的。

假设存在一个超平面 $w^{1T}x + b^1 = 0$ 设其距离支持向量 $(x_i, y_i)$ 的距离为 $\gamma$ .

则有 \(\frac{ y_i ( w^{1T}x_i + b^1 ) }{ \begin{Vmatrix} w^1 \end{Vmatrix}} = \gamma\) 两边同除 $\gamma$ , ( $y_i$ 保证正号 )

则有 $\frac{ y_i ( w^{1T}x_i + b^1 ) }{ \gamma \begin{Vmatrix} w^1 \end{Vmatrix} } = 1$

引入 $w = \frac{ w^1 }{ \gamma \begin{Vmatrix} w^1 \end{Vmatrix} }$ , $b = \frac{ b^1 }{ \gamma \begin{Vmatrix} w^1 \end{Vmatrix} }$

则有 $y_i ( w^Tx_i + b ) = 1$ ,此时距离支持向量的距离为 $y_i ( \frac{ w^Tx_i + b }{ \begin{Vmatrix} w \end{Vmatrix} } ) = \frac { 1 }{ \begin{Vmatrix} w \end{Vmatrix} }$

我们想要到支持向量的距离最大化， 而这时候对于空间中任意样本 $y ( w^T x + b ) \geq 1$ ,

引出目标函数 :

\[\min_{ w,b } \frac{1}{2} \begin{Vmatrix} w \end{Vmatrix} ^2\]

限制条件 :

\[1-y_i(w^T x_i +b) \leq 0 , i = 1,2,...,N\]

软间隔与正则化

为了应对有些分类较困难的问题，我们引入了松弛变量的概念. 一般来说，对于可分割的情况， 有 $1-y_i(w^T x_i +b) \leq 0$ ,

为了让那些跑到对面的错误分类的数据满足这个公式。我们使用松弛因子 $\xi \geq 0$ ， 有 $1-y_i(w^T x_i +b) - \xi_{i} \leq 0, i = 1,2,…,N$ ,这样以后我们就可以容忍掉这些分类错误的数据，这也是起到了正则化的作用。

则目标函数重写为 :

\[\min_{ w,b,\xi } \frac{1}{2} \begin{Vmatrix} w \end{Vmatrix} ^{2} + C \sum_{i=1}^{m} \xi_i\]

限制条件 :

\[1-y_i(w^T x_i +b) - \xi_{i} \leq 0, i = 1,2,...,N\] \[\xi_i \geq 0, i=1,2,...,N\]

说明

1. 软间隔只是容忍掉部分错误分类的数据， 但是并不是指将分类错误的数据分类正确，模型的间隔面不变。
2. 通过限制松弛变量的极小值，来最大程度的保证模型的准确性， 防止欠拟合

对偶

这是一个凸优化问题， 目标函数是一个凸函数， 限制条件为线性函数。引入拉格朗日对偶函数 :

\[L(\alpha,\beta,w,b,\xi)=\frac{1}{2}\begin{Vmatrix}w\end{Vmatrix}^{2}+C\sum_{i=1}^{N}\xi_i+\sum_{i=1}^{N}\alpha_{i}[1-\xi_i-y_i(w^Tx_i+b)]-\sum_{i=1}^{N}\beta_{i}\xi_{i}\]

原问题转为 : \(\max_{\alpha,\beta}\min_{w,b,\xi}L(\alpha,\beta,w,b,\xi)\)

限制条件 :

\[\alpha_i \geq 0, i=1,2,...,N\] \[\beta_i \geq 0,i=1,2,...,N\] \[\alpha_{i}[1-\xi_i-y_i(w^Tx_i+b)]=0,i=1,2,...,N\] \[-\beta_{i}\xi_{i}=0,i=1,2,...,N\]

$\frac{\partial L}{\partial w}=0$ 推出 :

\[w-\sum_{i=1}^{m}\alpha_iy_ix_i=0\] \[w=\sum_{i=1}^{m}\alpha_iy_ix_i\tag{1}\]

$\frac{\partial L}{\partial b}=0$ 推出:

\[\sum_{i=1}^{N}\alpha_iy_i=0\tag{2}\]

$\frac{\partial L}{\partial\xi_i}=0$ 推出: \(C-\alpha_i-\beta_i=0\)

\[C=\alpha_i+\beta_i\tag{3}\]

将 $(1)(2)(3)$ 带回到 $L(\alpha,\beta,w,b,\xi)$ 函数

\[L(\alpha,\beta,w,b,\xi)=\sum_{i=1}^{N}\alpha_i-\frac{1}{2}\sum_{j=1}^{N}\sum_{i=1}^{N}\alpha_i\alpha_jy_iy_jx_i^Tx_j\]

求得对偶问题

\[\max_{\alpha }L(\alpha )=\sum_{i=1}^{N}\alpha_i-\frac{1}{2}\sum_{j=1}^{N}\sum_{i=1}^{N}\alpha_i\alpha_jy_iy_jx_i^Tx_j\]

限制条件 :

\[\alpha_i+\beta_i=C; i=1,2,...,N\] \[\sum_{i=1}^{N}\alpha_iy_i=0\] \[\alpha_i \geq 0; i=1,2,...,N\]

解出 $\alpha$ 以后,模型可以表示为 :

\[f(x)=w^{T}x+b=\sum_{i=1}^{N}\alpha_iy_ix_i^Tx+b\]

SMO

对于上面问题可以使用二次规划算法解决，但在实际应用中由于样本数量较多可能造成很大开销。为了避开这个障碍，人们通过利用问题本身的特性提出了较为高效得算法。 SMO 算法就是其中之一。

SMO 算法是先固定 $\alpha_i$ 之外的所有参数，然后求 $\alpha_i$ 上的极值。

但是考虑到了约束条件 $\sum_{i=1}^{N}\alpha_iy_i=0$ ，若固定了 $\alpha_i$ 之外的其他变量， 则 $\alpha_i$ 也固定 : $\alpha_i=y_i\sum_{j\neq i}\alpha_jy_j$

于是，SMO每次选择两个变量 $\alpha_i$ , $\alpha_j$ 并固定其他参数。

我们先推导一下关于 $\alpha_i$ , $\alpha_j$ 的优化公式:

选取 $\alpha_i$ , $\alpha_j$ 后, 假定其他参数为常数

另导函数等于零，计算得到

\[\alpha_1^{new}=\alpha_1^{old}+y_1y_2(\alpha_2^{old}-\alpha_2^{new})\]

优化步骤 :

1. 选取一对需要更新的变量 $\alpha_i$ , $\alpha_j$
2. 固定 $\alpha_i$ , $\alpha_j$ 以外的参数, 基于优化公式获取更新后的 $\alpha_i$ 和 $\alpha_j$

注意到只选取的 $\alpha_i$ 和 $\alpha_j$ 中有一个不满足KKT条件，目标函数就会在迭代后增大。直观来看，KKT条件违背的程度越大， 则变量更新后可能导致目标函数值增幅越大。于是，SMO先选取违背KKT条件程度最大的变量。第二个变量赢选择一个使目标函数增长最快的变量，但由于比较各变量所对应的目标函数值增幅的复杂度过高，因此SMO采用了一种启发式：使选取的两变量所对应样本之间的间隔最大。一种直观的解释使，这样的两变量有很大的差别，与对两个相似的变量进行更新相比，对他们进行更新会带给目标函数值更大的变化。

优化时需要考虑限制问题

因为在限制条件中存在 : $\alpha_i+\beta_i=C$ ( $0 \leq \alpha_i \leq C$ ) , $\alpha_iy_i+\alpha_jy_i=\xi,\xi为常数$

$0\leq\alpha_i\leq C$ 将两变量限制在 $[0,C]*[0,C]$ 的矩阵中, $\alpha_1y_1+\alpha_2y_2=\xi$将两个变量限制在矩形中平行于对角线的线段上。 因为要考虑 $y_1,y_2$ 的符号(斜率) 所以有两种情况，如上。

那么 $\alpha_2^{new}$ 必须要在方框内且在直线上取得。假设 L 和 H 分别是上图中 $\alpha_2^{new}$ 所在的线段的边界。那么：

\[L\leq\alpha_2^{new}\leq H\]

对于上面左图中的情况 $y_1\neq y_2$ ，则

\[L=\max(0,\alpha_2^{old}-\alpha_1^{old})\] \[H=\min(C,C+\alpha_2^{old}-\alpha_1^{old})\]

对于上面右图中的情况 $y_1=y_2$ , 则

\[L=\max(0,\alpha_2^{old}+\alpha_1^{old}-C)\] \[L=\max(C,\alpha_2^{old}+\alpha_1^{old})\]

b 的求解

---

求解完 $\alpha,b$ 以后，我们的模型可以表示为 :

\[f(x) = \sum_{i=1}^{N}\alpha_iy_ix_i^Tx+b\]

分割超平面为 :

\[\sum_{i=1}^{N}\alpha_iy_ix_i^Tx+b=0\]

核函数

核函数为处理线性不可分的数据集划分提供了方法, 例如对于异或问题：

在正常情况下，我们无法通过寻找一个超平面来正确分割样本， 可以考虑将二维样本映射到三维。

定义线性映射 $\phi(x)=[x_1,x_2,(x_1-x_2)^2]$ , 此时 $\phi(x)$ 样本映射空间内，便可以寻找分割超平面。

有证明，如果原始空间使有限维，那么一定存在一个高维特征空间使样本可分。(证明略)

在实际情况下，寻找 $\phi(x)$ 是困难的，映射特征空间维数很高，可能到无限维。 而且在svm中我们也无需直接获得 $\phi(x)$ , 只需要它的内接表示

\[k(x_i, x_j)=<\phi(x_i), \phi(x_j)>=\phi(x_i)^T\phi(x_j)\]

$k(x_i, x_j)$ 称为核函数

对于核函数情况下的对偶可以重写为 :

\[\max_{\alpha }L(\alpha )=\sum_{i=1}^{N}\alpha_i-\frac{1}{2}\sum_{j=1}^{N}\sum_{i=1}^{N}\alpha_i\alpha_jy_iy_jk(x_i,x_j)\]

常见的核函数:

代码案例

简单描述一下训练过程， 采用的莺尾花样本集，无松弛因子的情况

##
#
# svm 算法
#
##

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA
import numpy as np
import random
import matplotlib.pylab as plt

def func_dot(x_i:np, x_j:np) -> float :
    """
    核函数
    :param x_i:
    :param x_j:
    :return:
    """
    # 线性核
    return np.dot(x_i.T, x_j)


def svm_f(X:np, Y:np, alpha:np, b:float, x_i:np):

    """
    计算 f(x)
    :param x:
    :param alpha:
    :param y:
    :param x_i:
    :return:
    """

    Y = np.mat(Y)
    X = np.mat(X)
    x_i = np.mat(x_i)
    alpha = np.mat(alpha)

    A = np.multiply(Y, alpha)

    x_matric = np.dot(X, x_i.T)
    res = np.dot(A, x_matric) + b

    return res

def select_j(i, m):
    while True:
        j = random.randint(0, m-1)
        if j != i :
            return j


def model(X:np, Y:np):
    """
    SVM 模型训练
    """

    n_sample = X.shape[0]
    n_vector = X.shape[1]
    max_iter = 6

    alpha = np.linspace(0, 0, n_sample)

    b = 0

    for _ in range(max_iter) :
        for i in range(n_sample) :
            j = select_j(i, n_sample)


            x_i = X[i,:]
            x_j = X[j,:]

            ETA = np.dot(x_j, x_j.T) + np.dot(x_i, x_i.T) - 2*np.dot(x_i, x_j.T)

            if ETA <= 0 :
                continue

            E_i = svm_f(X, Y , alpha, b, x_i) - Y[i]
            E_j = svm_f(X, Y, alpha, b, x_j) - Y[j]

            alpha_i_new = alpha[i] + Y[i] * (E_j - E_i) / ETA

            alpha_i_new = max(0, alpha_i_new)

            alpha_j_new = alpha[j] + Y[i]*Y[j] * (alpha[i] - alpha_i_new)

            alpha_j_new = max(0, alpha_j_new)


            b_j_new = - E_j - Y[j] * func_dot(x_j, x_j) * (alpha_j_new - alpha[j]) - Y[i] * func_dot(x_i, x_j) * (alpha_i_new - alpha[i]) + b

            b_i_new = -E_i - Y[i] * func_dot(x_i, x_i) * (alpha_i_new - alpha[i]) - Y[j] * func_dot(x_i, x_j) * (alpha_j_new - alpha[j]) + b


            if alpha_i_new > 0  :
                b = b_i_new
            elif alpha_j_new > 0 :
                b = b_j_new
            else:
                b = (b_i_new + b_j_new)/2


            alpha[i] = alpha_i_new
            alpha[j] = alpha_j_new

    # b = bair_clac(X, Y, alpha)


    return alpha, b


def model_test(train_x, train_y , test_x, test_y, alpha, b):
    """
    模型性能测试
    :param train_x:
    :param train_y:
    :param test_x:
    :param test_y:
    :param alpha:
    :param b:
    :return:
    """

    n_sample = test_x.shape[0]

    error_count = 0

    for i in range(n_sample) :
        y_hat = svm_f(train_x, train_y, alpha, b, test_x[i])

        if (y_hat * test_y[i]) <= 0 :
            error_count = error_count + 1

    return error_count/n_sample


def get_w(X:np , Y:np, alpha:np) -> np :
    """
    得到 w 参数
    :param X:
    :param Y:
    :param alpha:
    :return:
    """


    X = np.mat(X)
    Y = np.mat(Y)
    alpha = np.mat(alpha)


    param = np.multiply(Y.T, alpha.T)

    w_matric = np.multiply(param, X)

    w  = np.sum(w_matric, axis=0)

    return w

if __name__ == '__main__':

    # 加载莺尾花数据集
    iris = load_iris()


    # 数据处理
    X = iris.data
    Y = iris.target
    X = X[Y!=2, :]
    Y = Y[Y!=2]


    Y[Y==0] = -1

    train_x, test_x, train_y, test_y = train_test_split(X, Y, test_size=0.3)


    alpha, b = model(train_x, train_y)

    print(alpha, b)

    err_ratio = model_test(train_x, train_y, test_x, test_y, alpha, b)

    print("error ratio : {0}".format(err_ratio))

---

附录 : 对偶定理

目标函数 :

\[\minf(w)\]

限制条件 :

\[g_i(w) \leq 0, i=1,2,...,K\] \[h_i(w)=0,i=1,2,..,M\]

对偶问题 :

\[L(w,\alpha,\beta)=f(w)+\sum_{i=1}^{k}\alpha_ig_i(w)+\sum_{j=1}^{M}\beta_jh_j(w)\]

原函数的对偶表示为:

\[\max \lbrace \theta(\alpha,\beta)=inf_w[L(w,\alpha,\beta)] \rbrace\]

最小最大问题: 对于每个固定的 $\alpha$ , $\beta$ 都有一个 $w^”$ , 使得 $L(\alpha, \beta, w)$ 去的最小， 然后遍历所有的 $(\alpha,\beta, w^”)$ 使得 $L$ 取最大。 对应的为 $(\alpha^”,\beta^”,w^”)$

---

说明

• 代码采用特征为连续属性莺尾花样本集
• 参考 [周志华-机器学习]
• 参考 浙江大学-研究生机器学习课程
• 参考 攀登传统机器学习的珠峰-SVM